3

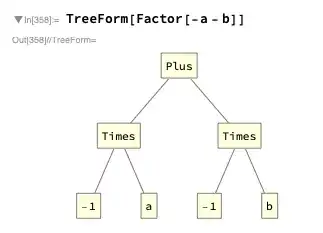
Consider the two expressions -2a-2b and -a-b. The TreeForm[] looks identical

enter image description here enter image description here

However, Factor[] does not give an identical new structure what I would expect

enter image description here enter image description here

Why can/does Mathematica not factor the -1?

I am interested in getting the output of an expression like I would write it without using low-level box operations because I want to be able to use TeXForm[].

UPDATE
This question came up in my other question https://mathematica.stackexchange.com/a/203451/13042

I have reduced my representation problem to following input

list = {2 (j - Subscript[j, 2] - Subscript[j, 3] + Subscript[j, 6]), -b - 
  Subscript[b, 2] - 3 Subscript[b, Subscript[\[Sigma], d]] - 
  3 Subscript[b, Subscript[\[Sigma], v]], 12}

$$\left\{2 \left(j-j_2-j_3+j_6\right),-3 b_{\sigma _d}-3 b_{\sigma _v}-b-b_2,12\right\}$$

With

HoldForm[+##] & @@ list

I get

$$2 \left(j-j_2-j_3+j_6\right)+\left(-b-b_2-3 b_{\sigma _d}-3 b_{\sigma _v}\right)+12$$

The remaining issue is that I want to have a minus sign between parentheses if the first term in the second parenthesis has a minus sign. The final result should look like

$$2 \left(j-j_2-j_3+j_6\right)-\left(b+b_2+3 b_{\sigma _d}+3 b_{\sigma _v}\right)+12$$

And to be clear this is just one example. I have several expressions which I want to output in a similar way. If it would be only one, I would not bother and would simply do it manually. Also writing the expression with a minus sign emphasizes the similar structure to the expression 2j-b where the above given is an advanced version of.

(A related annoyance is that Inactivate[2 - 2] gives 2 + -2. Please do not focus on this: it is not really important for my primary question here and might make the discussion less focused).

Hotschke
  • 707
  • 3
  • 11
  • 2
    A related annoyance is that Inactivate[2 - 2] gives 2 + -2 for this one, you need to activate anything that returned by Inactivate. So Activate@Inactivate[2 - 2] gives 0. I think the + - part comes from what helps says: Inactivate replaces all instances of f with Inactive[f] for symbols f used as heads in expr – Nasser Aug 10 '19 at 09:20
  • Because in Mathematica, -1(a+b) and -(a+b) are automatically converted to -a-b. – Somos Aug 10 '19 at 12:40
  • The question is why does Mathematica do this and not for -2(a+b)? – Hotschke Aug 10 '19 at 12:44
  • Long ago the developers of Mathematica decided to make certain automatics simplifcations for whatever reasons and due to backwards compatibility that will never change. Perhaps your real questions should be how to get around this "feature" for some specific situations. – Somos Aug 10 '19 at 13:26
  • And there is also no switch to change it temporarily? I have added more details to the question. Do you know how to factor out the minus sign? – Hotschke Aug 10 '19 at 13:41
  • TeXForm@*HoldForm@*Times @@ Power @@@ FactorList[-(a + b)]? – Michael E2 Aug 10 '19 at 14:10
  • 1
    BTW, re "I am interested in getting the output of an expression like I would write it...": not exactly a strength of M, since canonicalization of expressions is (currently) an important principle in the construction of efficient symbolic algebra algorithms. – Michael E2 Aug 10 '19 at 16:57
  • FactorList might give a result more to your liking. – Daniel Lichtblau Aug 10 '19 at 18:00

0 Answers0