find a maximum parameter for a range of target eigenvalues as a function of matrix dimension

Question

I have a symbolic tridiagonal matrix of this form

a = 0;
c = 0.25;
sa1[b_] :=SparseArray[{Band[{1, 1}] -> a, 
          Band[{2, 1}, {2 l, 2 l}] -> {I b/4, I c}, 
          Band[{1, 2}, {2 l, 2 l}] -> {-I b/4, -I c}}, {2 l, 2 l}];

where a and c are fixed parameters, b>0 is a varying parameter and l is the rank of the matrix. By diagonalizing this matrix as a function of b, I can obtain the largest value for b, let's say bmax, such that the absolute value of the eigenvalues is less than 1/10^5. Note that the eignevalues always appear in pairs by symmetry. To find bmax, I have employed the Arnoldi method which has been employed also in this thread

closestEVtotarget[b_?NumericQ, target_?NumericQ] := 
  Abs[First@
    Eigenvalues[sa1[N[b]], -1, 
     Method -> {"Arnoldi", "Criteria" -> "Magnitude", 
       "Shift" -> target}]];
With[{target = 1/10^5}, 
  Plot[closestEVtotarget[b, target], {b, 0, 0.5}, 
   GridLines -> {None, {target}}]];
With[{target = 1/10^5}, 
  plot = Plot[{target, closestEVtotarget[b, target]}, {b, 0, 2}]; 
  bmaxval = Graphics`Mesh`FindIntersections[plot]];

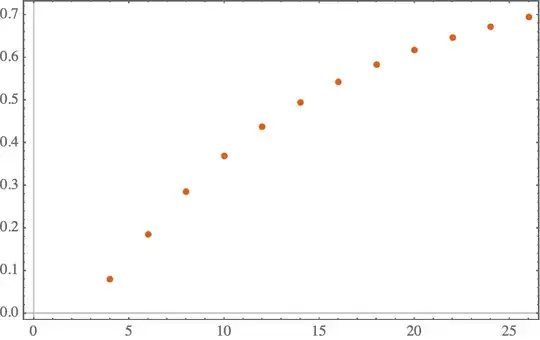
For instance for l=6, printing the bmaxval would be

{{0.185999,0.00001}}

where bmax=0.185999. Now the question is how I can collect all bmax values for different even values of l, let's say

llist = {4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26};

and plot l vs. bmax?

Answer 1

define the matrix with memoization:

a = 0;
c = 0.25;
sa1[l_Integer] := sa1[l] = Function[b, 
  Evaluate@SparseArray[{Band[{1, 1}] -> a, 
    Band[{2, 1}, {2 l, 2 l}] -> {I b/4, I c}, 
    Band[{1, 2}, {2 l, 2 l}] -> {-I b/4, -I c}}, {2 l, 2 l}]]

calculate the smallest eigenvalue by absolute value:

ev[l_Integer, b_?NumericQ] := Eigenvalues[sa1[l][b], -1, Method -> "Arnoldi"][[1]]

find the spot where the smallest eigenvalue is equal to $10^{-5}$:

Table[{l, b /. FindRoot[ev[l, b] == 10^-5, {b, 0.5}]}, {l, 4, 26, 2}]

{{4, 0.0796537}, {6, 0.18602}, {8, 0.285008}, {10, 0.368593}, {12, 0.437727}, {14, 0.494971}, {16, 0.542751}, {18, 0.583032}, {20, 0.617337}, {22, 0.646833}, {24, 0.672422}, {26, 0.6948}}

ListPlot[%]