0

My code is 

data = {{0, 0.00355}, {6, 0.00343}, {9, 0.00331}, {48, 0.00319}, {173, 0.00308}, {200, 0.00308}};
fun= FindFit[data, a*Exp[b*(x)] + c, {a, b, c}, x]
p[x_] := a*Exp[b*x] /. fun

This gives me {a -> -3.2091*10^-91, b -> 1., c -> 0.003312}

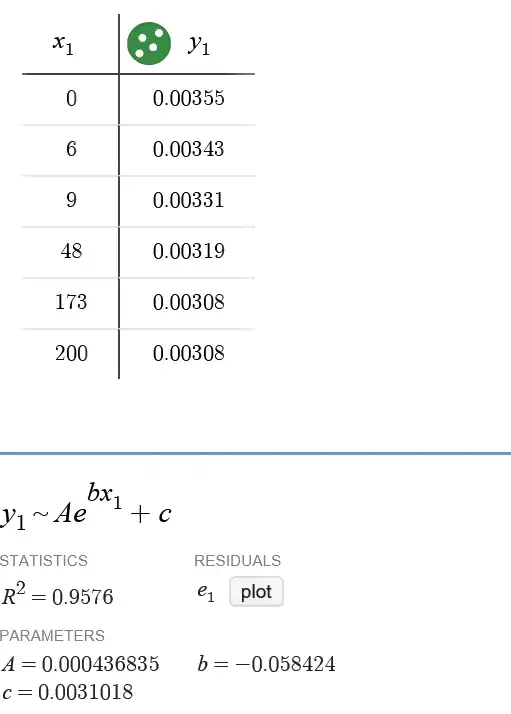
whereas when I use desmos it gives me: desmos

where a=0.000437, b=-0.0598, and c=0.00310.

Desmos also gives the same answer as when I put it into wolfram alpha. I just want to know why my mathematica doesn't give me the same result and how I can make it give me the same as desmos. I have a lot of other data I would like to process in the same way and doing it all in desmos would be too painful.

matthaigh27
  • 3
  • 1
  • Giving better starting values works: FindFit[data, a*Exp[b*(x)] + c, {a, {b, -1}, c}, x]. – JimB Aug 28 '19 at 00:59
  • Try this NonlinearModelFit[data, a Exp[b x] + c, {a, b, c}, x, Method -> {NMinimize, Method -> "DifferentialEvolution"}, MaxIterations -> 1000] – OkkesDulgerci Aug 28 '19 at 02:35

1 Answers1

3

It just failed to converge (or rather, it converged to a bad fixed point). Use Exp[-b x] instead of Exp[b x]; this time it works as expected:

NonlinearModelFit[data, a Exp[-b x] + c, {a, b, c}, x]
(* {a -> 0.000436835, b -> 0.0584236, c -> 0.0031018} *)

Also, use NonlinearModelFit instead of FindFit (see here for more details).

AccidentalFourierTransform
  • 10,279
  • 1
  • 19
  • 51
  • I pasted your code in and it gave me:

    General::munfl: -7.998810^-8/-6.27792228664020110^7320 is too small to represent as a normalized machine number; precision may be lost.

    General::munfl: 3.999410^-8/3.13896114332010110^7320 is too small to represent as a normalized machine number; precision may be lost.

    General::munfl: -6.8855610^-8/-1.86448385339743410^5969 is too small to represent as a normalized machine number; precision may be lost.

    General::stop: Further output of General::munfl will be suppressed during this calculation.

     – matthaigh27 Aug 28 '19 at 00:01
  • @Toadfuture huh, that's weird. Can you restart your kernel (run Quit[]) and try again? It works for me... – AccidentalFourierTransform Aug 28 '19 at 00:05
  • I quit the kernel and the errors still showed up but the fitted model output was what I wanted so I guess that's all I need. Thank you so much for your help! – matthaigh27 Aug 28 '19 at 00:08
  • @Toadfuture A few messages about underflow may not be a serious problem: it just indicates that machine numbers were flushed to zero during intermediate calculations, which can happen when you use exponents. If the returned fit is good you don't need to worry about it. – Sjoerd Smit Aug 28 '19 at 08:41
  • @AccidentalFourierTransform Method->"NMinize"although solves the first case "...Exp[+b x]": NonlinearModelFit[data, a Exp[ b x] + c, {a, b, c}, x, Method -> "NMinimize"] – Ulrich Neumann Aug 28 '19 at 12:56