5

Subsequent I consider the transient heat exchange problem of a ring in polar coordinates.

The ring is heated in a small range 0<\[CurlyPhi]<20° and cooled along the rest of the circumference.

The Method of Lines together with PeriodicBoundaryConditions nearly solves the problem as expected: 

tsim = 10; \[CapitalDelta]\[CurlyPhi] = 20 Degree; Tu = 20 ; T0 = 100;
U = NDSolveValue[{   Derivative[1, 0 ][u][t, \[CurlyPhi]] + .1 Derivative[0, 1  ][u][t, \[CurlyPhi]] == .1 Derivative[0, 2][u][t, \[CurlyPhi]]+ 25  Boole[0 < \[CurlyPhi] < \[CapitalDelta]\[CurlyPhi]] (* heating *)- .1 Boole[\[CapitalDelta]\[CurlyPhi] < \[CurlyPhi] < 2 Pi] (u[t, \[CurlyPhi]] - Tu) (* couling*), u[0, \[CurlyPhi]] == T0 (*ic*), PeriodicBoundaryCondition[u[t, \[CurlyPhi]], \[CurlyPhi] == 2 Pi, Function[{x}, x - 2 Pi]]},
u,{\[CurlyPhi], 0, 2 Pi}, {t, 0, tsim}
, Method -> {"MethodOfLines", "TemporalVariable" ->t,"SpatialDiscretization" -> {"FiniteElement"}}]

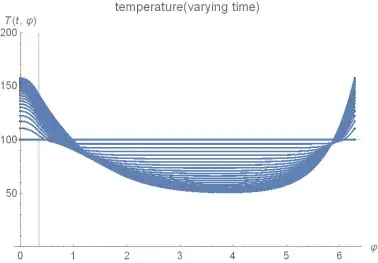
Plot[Table[U[t, \[CurlyPhi]], {t, Subdivide[0, tsim, 20]}], {\[CurlyPhi], 0,2 Pi}, GridLines -> {{\[CapitalDelta]\[CurlyPhi]}, {T0}},PlotRange -> {0, 200}, PlotLabel -> "temperature(varying time)",AxesLabel -> {\[CurlyPhi], T[t, \[CurlyPhi]]}, AxesOrigin -> {0, 0}]

enter image description here

As you can see, probably due to the imposed PeriodicBoundaryCondition, the slope of the temperature at \[CurlyPhi]==0 is zero and different to the slope at \[CurlyPhi]==2Pi .

For physical reasons I would expect a solution with periodic slope.

My question:

How can I force NDSolve to give a periodic solution u[t,0]==u[t,2Pi] and D[u[t,0],\[CurlyPhi]]==D[u[t,2Pi],\[CurlyPhi]]

Thanks!

MelaGo
  • 8,586
  • 1
  • 11
  • 24
Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55
  • 1
    I guess the underlying issue is related to those mentioned in: https://mathematica.stackexchange.com/q/188109/1871 https://mathematica.stackexchange.com/a/202287/1871 If you turn to the traditional TensorProductGrid e.g. u[t, 0] == u[t, 2 Pi] and Method -> {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 100, "MinPoints" -> 100, "DifferenceOrder" -> 4}} the result will be the desired one. – xzczd Sep 02 '19 at 10:36
  • @xzczd Thank you very much, the version with TensorProductGrid without PeriodicBoundaryCondition seems to be the right one! – Ulrich Neumann Sep 02 '19 at 10:59

1 Answers1

3

To the best of my knowledge, with the finite element method you can not. The reason is that there is no way to have no boundary condition at some portion of the boundary. Either a boundary condition is specified on input (with the equations) then that is used or none is given which then results in a Neumann zero implicitly used. To the best of my knowledge there is no way to avoid that. That's inherent in the finite element method and its derivation.

Henrik Schumacher
  • 106,770
  • 7
  • 179
  • 309
user21
  • 39,710
  • 8
  • 110
  • 167
  • Do you mean that, PeriodicBoundaryCondition only imposes periodic b.c. for the function (in this case u) and doesn't take care about derivative of the function (in this case Derivative[0,1][u]), and simply use a zero NeumannValue (at the left boundary, I guess?) to complement the missing part? – xzczd Sep 02 '19 at 13:26
  • @xzczd, no. Let me explain, but first forget Derivative[0,1][u] in the context of FEM boundary conditions. It will confuse you, the only derivative type boundary condition in the FEM context is NeumannValue and this is tied to the equation in a very special way. See here and here. – user21 Sep 02 '19 at 13:49
  • @xzczd, Now, for a PBC in 1D there is an equation stiffness[[n+1,All]]=0; stiffness[[n+1,1]]=1;stiffness[[n+1,-1]]=-1; giving an equation u[leftbc]==u[rightbc]. But there is also the implicit NeumanValue or some other BC. This comes from the derivation (see link above) you'd need to compensate that contribution to make this work. So it's not so much the PBC that is the problem but that FEM does not allow for no boundary condition. If nothing is specified there is always an implicit Neumann zero. I hope this makes this a bit clearer. – user21 Sep 02 '19 at 13:52
  • Er… Is there any plan to, say, include some explanation in the Possible Issues section of document of PeriodicBoundaryCondition? The difference between periodic b.c. implemented in TensorProductGrid and FiniteElement is rather confusing, at least for me. Or their behavior will finally be the same in future versions? – xzczd Sep 03 '19 at 05:14
  • @ I have updated the documentation of the PBC ref page. To the best of my knowledge the implementations can not be the same. But feel free to experiment if you can come up with a unification, let me know and I'll implement that. – user21 Sep 03 '19 at 07:12