2

The solution to $y'=x \ln(y)$ with initial conditions $y(1)=1$ is $y=1$.

How to persuade DSolve to obtain this solution?

ClearAll[y, x];
ode = y'[x] == x Log[y[x]];
ic = y[1] == 1;
sol = DSolve[{ode, ic}, y[x], x]

Mathematica graphics

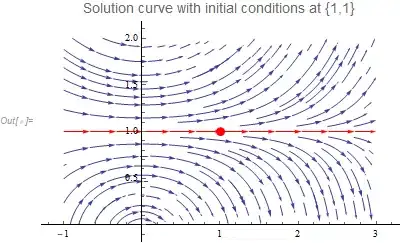
One can see that $y=1$ is solution that also satisfies the ic by looking at direction field.

ClearAll[x, y];
fTerm = x Log[y];
StreamPlot[ {1, fTerm}, {x, -1, 3}, {y, 0, 2},
 Axes -> True,
 Frame -> False,
 PlotTheme -> "Classic",
 AspectRatio -> 1 / GoldenRatio,
 StreamPoints -> {{{{1, 1}, Red}, Automatic}},
 Epilog -> {{Red, PointSize[.025], Point[{1, 1}]}},
 PlotLabel -> Style[Text[Row
    [{"Solution curve with initial conditions at {", 1, ",", 1,"}"}]], 14]
 ]

enter image description here

V 12.0 on windows 10

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • The function y[x]=1 is a singular solution of the ODE under consideration which cannot be obtained from its general solution y[x]->(LogIntegral^(-1))[x^2/2+Subscript[[ConstantC], 1]] produced by DSolve[y'[x] == x Log[y[x]], y[x], x]. Every soft has its limitations. – user64494 Sep 02 '19 at 12:01
  • It's the limit of the general solution as C[1] -> -Infinity, but M does not seem to be very robust with respect to the inverse function of LogIntegral[]. Related: https://mathematica.stackexchange.com/questions/57910/dsolve-not-finding-solution-i-expected – Michael E2 Sep 02 '19 at 12:26
  • @Michael E2: it's unclear whether the limit of the general solution as C[1] -> -Infinity is a solution of the ODE under consideration. This should be based. I don't think the proff is simple. In any case that limit is not a particular solution. – user64494 Sep 02 '19 at 13:40
  • @user64494 Pointwise convergence seems pretty clear to me. Just think about it. – Michael E2 Sep 02 '19 at 13:50
  • @Michael E2: I prefer arguments and references over ungrounded words. – user64494 Sep 02 '19 at 13:56
  • 2
    @user64494 Yes, so do I, but I would not want to deprive you of the pleasure of figuring it out. – Michael E2 Sep 02 '19 at 13:59
  • @Michael E2: In any case Limit[(LogIntegral^(-1))[x^2/2+Subscript[[ConstantC], 1]],Subscript[[ConstantC], 1]->-Infinity] fails. – user64494 Sep 02 '19 at 14:18
  • Let us continue this discussion in chat. – Michael E2 Sep 02 '19 at 14:28

1 Answers1

5

AsymptoticDSolveValue (introduced in V11.3) seems to be more robust than DSolve here and confirms (or at least not falsifies) the solution you want (as @MichaelE2 points out we cannot really get a rigorous solution from a finite series expansion this way):

AsymptoticDSolveValue[
  {y'[x] == x Log[y[x]], y[0] == 1}, 
  y[x], {x, 0, (*arbitrarily high finite order*) 10}
]

1

or to see how this works we can get the series expression in x before taking the limit $x\to 0$

AsymptoticDSolveValue[
  {y'[x] == x Log[y[x]], y[0] == y0}, 
  y[x], {x, 0, 2}
]
Limit[Evaluate[%], y0 -> 1]

y0 + 1/2 x^2 Log[y0]

1

Thies Heidecke
  • 8,814
  • 34
  • 44
  • 1
    I think there's a problem claiming this shows y[x] == 1 is a solution, when you've used only finitely many terms of the series. – Michael E2 Sep 02 '19 at 12:55
  • @MichaelE2 You're totally right, this kind of solution is very hand-wavy and should not be seen as a substitute for a rigorous proof, but more seen as an engineering technique to make the solution that we already suspected more plausible. – Thies Heidecke Sep 02 '19 at 12:59
  • plus usually solutions like y[x] == 1 here is theoretically easy to check but numerically unstable. – yshk Sep 02 '19 at 15:24