4

I am creating Euler's method for $\frac{dw}{dt}=(3-w)(w+1)$ for $\Delta t=0.5$ from $0\le t \le 3$. I tried the following.

S[w_, t_] := (3 - w)*(w + 1)
S[0, 0] := 3
h = 0.5
S[w + 1, t] == w + h*S[w, t]
P[m_] := S[m, m]
Table[P[x], {x, 0, 3/(0.5)}]

Which gives

out[321]= 0.5
out[322]= {3, 3, 3, 0, -5, -12, -21}

However, I doubt this is the correct answer. What should I do instead?

Arbuja
  • 59
  • 4
  • 18

1 Answers1

7

You have to define the recursive increment. (I assume in your code S[w + 1, t] == w + h*S[w, t] is related to that.)

F[w_, t_, h_] := w + h*S[w, t]

{h, n} = {0.1, 20};
pnts = NestList[{#1[[1]] + h, F[#1[[2]], #1[[1]], h]} &, {0, 0}, n];

ListLinePlot[pnts, PlotRange -> All]

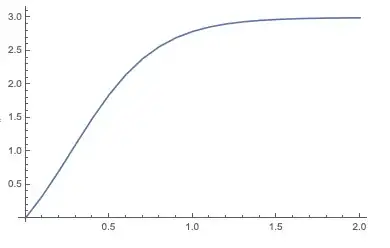
enter image description here

Here we verify.

sol = First[
  Flatten[f /. 
    DSolve[{f'[t] == Evaluate[S[f[t], t]], f[0] == 0}, f, t]]]

(* Function[{t}, (3 (-1 + E^(4 t)))/(3 + E^(4 t))] *)

ListLinePlot[Transpose[{pnts[[All, 1]], sol /@ pnts[[All, 1]]}]]

enter image description here

Anton Antonov
  • 37,787
  • 3
  • 100
  • 178
  • I tried using your code S[w_, t_] := (3 - w)*(w + 1) F[w_, t_, h_] := w + h*S[w, t]

    {h, n} = {0.1, 20}; pnts = NestList[{#1[[1]] + h, F[#1[[2]], #1[[1]], h]} &, {0, 0}, n];

    ListLinePlot[pnts, PlotRange -> All] but instead get ListLinePlot::lpn General::stop NestList::intnm ListLinePlot::lpn NestList::intnm NestList::intnm Set::altno NestList::intnm NestList::intnm How do we fix this?

     – Arbuja Sep 12 '19 at 16:15
  • I have no problems running this code : S[w_, t_] := (3 - w)*(w + 1); F[w_, t_, h_] := w + h*S[w, t]; {h, n} = {0.1, 20}; pnts = NestList[{#1[[1]] + h, F[#1[[2]], #1[[1]], h]} &, {0, 0}, n]; ListLinePlot[pnts, PlotRange -> All] – Anton Antonov Sep 12 '19 at 16:49
  • Never mind, I made a careless mistake : | – Arbuja Sep 12 '19 at 17:00