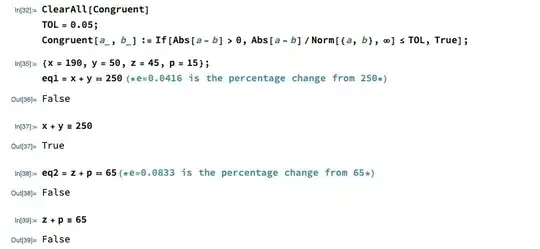
Given two equality constraints: x+y==250 and z+p==65 where x=190, y=50, z=45, p=15, I want to specify an error-tolerance level of e=0.05 below which the first equality should be TRUE and above which the second equality be FALSE.
{x=190, y=50, z=45, p=15};
eq1= x+y==250; (* e=0.0416 is the percentage change from 250*)
eq2= z+p==65; (* e=0.0833 is the percentage change from 65*)
(*Mathematica output*)
(*FALSE, FALSE*)
(*I like to receive for given e=0.05*)
(*TRUE, FALSE*)
How can I set the error-tolerance level of e=0.05 for the two constraints?
Any idea?
$EqualTolerancewould be that you do not want to use machine precision floats, but would like something that works on, say, exact input such as shown (except fore=0.05). Otherwise, it does what you desire:Block[{Internal`$EqualTolerance = MachinePrecision + Log10[0.05]}, {eq1 = x + y == 250., eq2 = z + p == 65.} ]– Michael E2 Sep 15 '19 at 19:24MachinePrecision+Log10[0.05]do? I know it generates the output I want, but I did not understand what your code does. – Tugrul Temel Sep 15 '19 at 22:40e=0.05, then I will assume that the equality holds. – Tugrul Temel Sep 16 '19 at 10:07