Identifying the three frequencies using fourier transform

Question

The following simple function has clearly three frequency components:

 fun[x_] = Cos[ x] + Cos[2 x] + Cos[3 x];
data = Table[fun[x], {x, 0, 2 \[Pi], 0.1}];
ListPlot[data, ImageSize -> 200]

How can one show these frequencies using the Fourier transform? I tried the following

ListLinePlot[Abs[Fourier[data]], PlotRange -> All, ImageSize -> 200]

But it doesn't seem to lead to the proper answer.

Edit: I would expect the Fourier plot to show three peaks corresponding to three frequencies in the ratio 1:2:3.

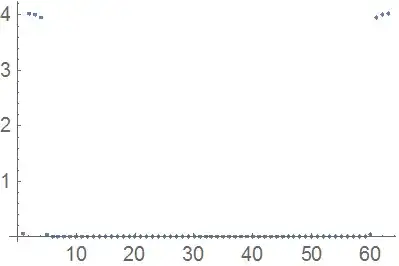
Try ListPlot instead of ListLinePlot and you'll see the both frequencies! — Ulrich Neumann, Sep 18 '19 at 09:39
@UlrichNeumann, thanks. With two frequencies, it was looking suspicious to me. Now with three frequencies, it is still showing two peaks with ListPlot. — Rob, Sep 18 '19 at 10:00
I have put some basic information on Fourier here which may help. Your three frequencies are a perfect match to your time interval and are multiples of the fundamental frequency so you get the first three points in the spectrum. — Hugh, Oct 18 '19 at 16:50

score 1 · Answer 1 · answered Sep 18 '19 at 10:05

1

ListPlotshows the frequencies:

fun[x_] = Cos[ x] + Cos[2 x] + Cos[3 x];
data = Table[fun[x], {x, 0, 2 \[Pi], 0.1}];
ListPlot[Abs[Fourier[data]], PlotRange -> All]

answered Sep 18 '19 at 10:05

Ulrich Neumann

Thanks. Shouldn't there be three peaks? – Rob Sep 18 '19 at 10:06
Yes, every point stands for a peak of the special frequency. – Ulrich Neumann Sep 18 '19 at 10:11
Then there are six frequencies depicted in this plot? – Rob Sep 18 '19 at 10:15
2

@Patrick No there are only three frequencies for your signal. More details you might find in Nyquist–Shannon sampling theorem – Ulrich Neumann Sep 18 '19 at 11:12

1 Answers1