3

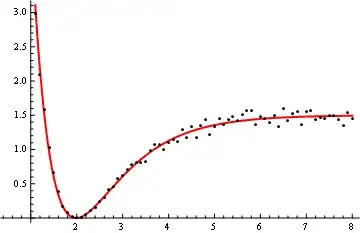
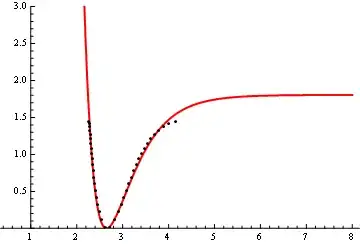
I am trying to fit data to a Morse potential using NonlinearModelFit as follows:

morse[r_] := d (1 - Exp[a (re - r)])^2;
nlm1 = NonlinearModelFit[data1, 
  d (1 - Exp[a (re - r)])^2, {d, {a, 1.5}, {re, 1.5}}, r]

However upon doing so I get the following error:

NonlinearModelFit::cvmit: Failed to converge to the requested accuracy or precision within 100 iterations.

I have tried using different values for my constant and it's puzzling that the data does not fit. Here is the data I am using currently: 

{"Internuclear Separation ()", "Potential Energy (eV)"}, {2.2678, 
  1.44954}, {2.274, 1.41403}, {2.2801, 1.3726}, {2.2864, 
  1.32543}, {2.2929, 1.27275}, {2.3, 1.2149}, {2.3077, 
  1.15223}, {2.3163, 1.08509}, {2.3258, 1.01378}, {2.3364, 
  0.938569}, {2.3482, 0.859714}, {2.3614, 0.777423}, {2.376, 
  0.691882}, {2.3924, 0.603253}, {2.411, 0.511677}, {2.4324, 
  0.417273}, {2.4577, 0.320146}, {2.4891, 0.220385}, {2.5321, 
  0.118071}, {2.6176, 0.0132722}, {2.7173, 0.0132722}, {2.834, 
  0.118071}, {2.9083, 0.220385}, {2.9715, 0.320146}, {3.0294, 
  0.417273}, {3.0844, 0.511677}, {3.1379, 0.603253}, {3.1909, 
  0.691882}, {3.2443, 0.777423}, {3.2987, 0.859714}, {3.3549, 
  0.938569}, {3.4136, 1.01378}, {3.4758, 1.08509}, {3.5424, 
  1.15223}, {3.6149, 1.2149}, {3.6949, 1.27275}, {3.7846, 
  1.32543}, {3.8867, 1.3726}, {4.0049, 1.41403}, {4.144, 1.44954}}

Any ideas?

rm -rf
  • 88,781
  • 21
  • 293
  • 472
anand
  • 31
  • 3
  • 2
    D is the built-in Mathematica function for taking a partial derivative. Bad idea to use it to name a parameter. – m_goldberg Mar 05 '13 at 03:29
  • 1
    It appears that NonlinearModelFit does not like Subscript[r, e] as a parameter name. Try substituting re and see if that doesn't help. – m_goldberg Mar 05 '13 at 04:07
  • @m_goldberg it doesn't like a lot of things. The reason, AFAICT, is that when the model is compiled, common subexpression elimination is rather more thorough than one would often like. I encountered this problem here, but couldn't solve it conclusively except by using a rather inconvenient brute force method. – Oleksandr R. Mar 06 '13 at 04:05
  • @m_goldberg example: load that package, then follow @belisarius's answer, except substitute nlm = TransformedFit[data, morse[d, a, Subscript[r, e], r], {{d, 1.5}, {a, 1.5}, Subscript[r, e]}, r, "FitFunction" -> NonlinearModelFit] and subsequently nlm[1, x] in the plot. Because the parameters have been renamed, the messages do not arise. But working with renamed parameters is more awkward, so it's a double-edged sword. – Oleksandr R. Mar 06 '13 at 04:19

1 Answers1

1

However it seems to work pretty well:

morse[d_, a_, re_, r_] := d (1 - Exp[a (re - r)])^2;
noisyMorse[d_, a_, re_, r_] := (# + RandomReal[{-#, #}]/10) &@ morse[d, a, re, r]

data = Table[{x, noisyMorse[3/2, 1, 2, x]}, {x, 1/2, 8, .1}];

nlm = NonlinearModelFit[data, morse[d, a, re, r], {{d, 1.5}, {a, 1.5}, re}, r]

Plot[nlm[x], {x, 1/2, 8}, Epilog :> Point[data], PlotStyle -> {Red, Thick}]

Mathematica graphics

nlm["ParameterTable"]

Mathematica graphics

as expected

Edit

Using your data:

nlm = NonlinearModelFit[data, morse[d, a, re, r], {{d}, {a}, {re, 2.8}}, r]

Plot[nlm[x], {x, 1/2, 8}, Epilog :> Point[data], PlotStyle -> {Red, Thick}]

Mathematica graphics

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
  • Hi, Thanks for your great responses using @belisarius's response I was able to get the code working however it seems now I keep getting "Unable to converge within 100 iterations" I will update the original question with my sample data. – anand Mar 06 '13 at 05:40
  • @anand See Edit, please – Dr. belisarius Mar 06 '13 at 23:05