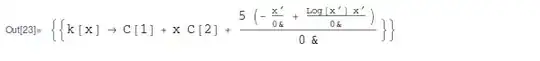1

I try to solve this second order ODE to get k:

$ \frac { \partial }{\partial z} ~ \frac{ \partial } {\partial \bar{z}}~ k[z, \bar{z}] = 5 $

Where z is complex coordinates, so to take the derivative for it, I have used ComplexD function defined in this thread:

What is the best way to define Wirtinger derivatives

So that the solution I have tried:

(* First: take the derivative *)

D[ ComplexD[k[Conjugate[z]], Conjugate[z]], z]

(* the output gives *)

Conjugate’[z] k’’[Conjugate[z]]

(* Second to solve I called Conjugate[z] by x *)

DSolve[ x’ k’’[x] == 5 , k[x], x]

Which gives:

enter image description here

The question :

  • Are these steps right? Sure there’s a better way for solution, but I don’t want to use NIntegrate.

  • What does & mean here ( i know it means pure function, but then what’s the value of k[x] ?

  • How to determine the value of k[x] for specific values of C[1] and C[2] ?

S.S.
  • 350
  • 1
  • 13

1 Answers1

2

In DSolve[ x' k''[x] == 5 , k[x], x] Mathematica interprets x' incorrectly.

Since $ \dfrac{\mathrm{d}[f(x)^*]}{\mathrm{d}x} = \biggl[\frac{\mathrm{d}f(x)}{\mathrm{d}x}\biggr]^* $ you can drop x' from your equation. Then 

{{sol}}=DSolve[ k''[x] == 5 , k[x], x]

gives you 

{{k[x] -> (5 x^2)/2 + C[1] + x C[2]}}

which does provide you with the solution of your differential equation that you can use like this: 

sol /. {C[1] -> 1, C[2] -> 3}

(* k[x] -> 1 + 3 x + (5 x^2)/2 *)

or like this

ksol = Function[{x}, Evaluate[k[x] /. sol /. {C[1] -> 1, C[2] -> 3}]]

(* Function[{x}, 1 + 3 x + (5 x^2)/2] *)

ksol[5]

(* 157/2 *)

or like this

ksol = Function[{x, c1, c2}, 
  Evaluate[k[x] /. sol /. {C[1] -> c1, C[2] -> c2}]]

(* Function[{x, c1, c2}, c1 + c2 x + (5 x^2)/2] *)

ksol[5, 1, 3]

(* 157/2 *)
Markhaim
  • 878
  • 4
  • 11
  • Thank you so much. – S.S. Sep 27 '19 at 05:48
  • @S.S. On the second thought I'm not so sure that's mathematically correct. There are some fishy moments: 1) why are you using two different derivatives in a 'D[ ComplexD[k[Conjugate[z]], Conjugate[z]], z]' ? 2) thought CompexD[ ComplexD[k[Conjugate[z]], Conjugate[z]], z] just gives 0... 3) d[f(x)∗]dx=[df(x)dx]∗ only for f: R->C which seems to not be true here 4) Trying to verify achieved solution by putting it into the original ODE D[ComplexD[ksol[Conjugate[z], 0, 1], Conjugate[z]], z] I got 5 D[Conjugate[z],z] which is equal to 5 iff D[Conjugate[z],z] == 1 which is questinable. – Markhaim Sep 27 '19 at 06:07