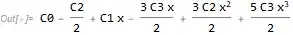Solve for coefficients to express polynomial in terms of another polynomial

Question

If I have a polynomial, say $p(x) = 6x^3 - x^2 + x$, and I want to express that in terms of a sum of other polynomials, how may I do that in Mathematica? Specifically I would like to say that $$p(x) = \sum_{i = 0}^3 \alpha_i P_i(x)$$ where $P_i(x)$ is the $i^{th}$ Legendre Polynomial (not super important what exactly the other polynomial is).

I have attempted the following:

p = 6*x^3 - x^2 + x;
Solve[p == (C3*LegendreP[3, x] + C2*LegendreP[2, x] + 
  C1*LegendreP[1, x] + C0*LegendreP[0, x]), {C3, C2, C1, C0}]

but it gives

 {{C0 -> x - C1 x - x^2 + 6 x^3 - 1/2 C2 (-1 + 3 x^2) - 
    1/2 C3 (-3 x + 5 x^3)}}

as the output when I know (for this example) the C's are real numbers.

This and this are related. – J. M.'s missing motivation Nov 15 '19 at 23:24 — J. M.'s missing motivation, Nov 15 '19 at 23:24

score 6 · Accepted Answer · edited Nov 16 '19 at 13:27

6

Please see if this does what you want.

p      = 6*x^3 - x^2 + x;
coeff  = CoefficientList[p, x]
p0     = Expand[C3*LegendreP[3, x] + C2*LegendreP[2, x] + C1*LegendreP[1, x] + 
              C0*LegendreP[0, x]];

Mathematica graphics

coeff0 = CoefficientList[p0, x];
eqs    = Thread[coeff == coeff0];

Mathematica graphics

sol = First @ Solve[eqs, {C0, C1, C2, C3}]

Mathematica graphics

To verify

 p0 /. sol

Mathematica graphics

edited Nov 16 '19 at 13:27

J. M.'s missing motivation

124,525
11
401
574

answered Sep 30 '19 at 03:02

Nasser

143,286
11
154
359

1

@C.Fuhrman - You have four unknowns so Solve needs four equations to determine them. As shown by @Nasser, the four equations are obtained by equating the corresponding coefficients. – Bob Hanlon Sep 30 '19 at 15:21

score 5 · Answer 2 · answered Sep 30 '19 at 15:30

5

Here's a different method using SolveAlways:

poly = 6 x^3 - x^2 + x
SolveAlways[poly == Sum[C[i] LegendreP[i, x], {i, 0, 3}], x]

{{C[0] -> -(1/3), C[2] -> -(2/3), C[1] -> 23/5, C[3] -> 12/5}}

answered Sep 30 '19 at 15:30

Sjoerd Smit

23,370
46
75

score 1 · Answer 3 · answered Sep 30 '19 at 06:18

1

This is the job of PolynomialReduce; see the documentation here.

For your example,

PolynomialReduce[p, Table[LegendreP[i, x], {i, 0, 3}], {x}]

is the idiomatic way. The output is of the form {coefficientList, remainder} where in the cases where the reduction is possible, remainder is zero.

answered Sep 30 '19 at 06:18

Marius Ladegård Meyer

6,805
1
17
26

This won't work though, because the multipliers can be (and are, in this case) polynomials in 'x'. One can homogenize everything to degree 3 however; that seems to work. Multiplying each degree in x by a distinct new variable is another way to go about this. – Daniel Lichtblau Oct 02 '19 at 16:47

score 1 · Answer 4 · answered Nov 15 '19 at 23:43

The classical method for converting a polynomial to an orthogonal basis is Salzer's algorithm. Adapted to the Legendre case, here is how to use it for conversion:

bb = CoefficientList[6 x^3 - x^2 + x, x]
   {0, 1, -1, 6}

Clear[a]; n = Length[bb] - 1;
a[0, 0] = a[1, 1] = bb[[n + 1]]; a[0, 1] = bb[[n]];
Do[a[0, k + 1] = bb[[n - k]] + a[1, k]/3;
   Do[a[m, k + 1] = (m + 1)/(2 m + 3) a[m + 1, k] + m/(2 m - 1) a[m - 1, k],
      {m, k - 1}];
   a[k, k + 1] = k/(2 k - 1) a[k - 1, k];
   a[k + 1, k + 1] = (k + 1)/(2 k + 1) a[k, k],
   {k, n - 1}];
Table[a[m, n], {m, 0, n}]
   {-1/3, 23/5, -2/3, 12/5}

Check:

%.LegendreP[Range[0, n], x] // Expand
   x - x^2 + 6 x^3

(Related math.SE answer.) – J. M.'s missing motivation Nov 16 '19 at 11:35 — J. M.'s missing motivation, Nov 16 '19 at 11:35

Solve for coefficients to express polynomial in terms of another polynomial

4 Answers4