11

The first three expressions evaluate as expected and the polynomial is displayed in what I would call "textbook" form. The last expression, however, switches the order of terms. Mathematica employs this change for two-term polynomials if it results in getting rid of the leading negative sign (at least that is the best I can deduce).

x^2 + x + 5 // TraditionalForm
(* x^2 + x + 5 *)

-x^2 + x + 5 // TraditionalForm
(* -x^2 + x + 5 *)

x^2 + x // TraditionalForm
(* x^2 + x *)

-x^2 + x // TraditionalForm
(* x - x^2 *)

These polynomials are the result of prior symbolic manipulation, so I cannot simply use HoldForm or the equivalent to maintain the desired order.

Is there a way to change this behavior in general so that the last expression displays as -x^2 + x? I can think of substitution rules to fix this particular example, but would like to find a robust solution that applies as transparently as possible across the board.

Edit

Additionally, PolynomialForm produces the same results:

PolynomialForm[-x^2 + x , TraditionalOrder -> True]
(* x - x^2 *)

PolynomialForm[-x^2 - x , TraditionalOrder -> True]
(* -x^2 - x *)

It seems that Mathematica will produce the traditional order for polynomial terms except when there are only two terms and reversing the order eliminates the leading negative sign.

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
RandomBits
  • 617
  • 4
  • 12
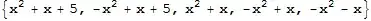
  • I was expecting to close this question with a reference to PolynomialForm[#, TraditionalOrder -> True] & but I see that you're going the other way. Let me think about that. – Mr.Wizard Mar 05 '13 at 23:41
  • @Mr.Wizard: Yes, I already tried PolynomialForm and that produces the same results. I will add that information to the question because that will probably be a common thought pattern. – RandomBits Mar 05 '13 at 23:45
  • Previous questions relating to this usually creates a new function to handle Plus. But would be nice with a way that lets you override the displayed order of Orderless arguments. – ssch Mar 06 '13 at 00:21
  • Previous questions: http://stackoverflow.com/questions/4109306/preventing-plus-from-rearranging-things http://stackoverflow.com/questions/3947071/controlling-order-of-variables-in-an-expression/3948995#3948995 – ssch Mar 06 '13 at 00:22
  • @ssch I don't think those solve this one (which I assume is why you didn't post an answer.) RandomBits doesn't want to prevent ordering, he wants to control it. – Mr.Wizard Mar 06 '13 at 00:46
  • Another related question:How to keep Collect[] result in order? – Jens Aug 03 '13 at 04:58

3 Answers3

7

Since the two other answers don't seem to do exactly what's needed, I'll try my luck:

order[poly_] := 
 Replace[Reverse@Sort[List @@ poly], List[x__] :> HoldForm[Plus[x]]]

order /@ {x^2 + x + 5, -x^2 + x + 5, x^2 + x, -x^2 - x}

$\left\{x^2+x+5,-x^2+x+5,x^2+x,-x^2- x\right\}$

Here I end up with HoldForm wrapping an expression that should have the sorted terms, and this ordering would be maintained when feeding it into TraditionalForm or TeXForm.

I avoided using Row for the output (and hence also don't use Format or MakeBoxes) so that I don't have to worry about getting things like $+\,-\,x$.

Jens
  • 97,245
  • 7
  • 213
  • 499
  • Well I was just getting around to this method myself but you were six minutes faster so +1. :-) – Mr.Wizard Aug 03 '13 at 05:37
  • Jens, do you see anything wrong with my second method? What do you see as the advantage or disadvantage of Sort[List @@ #] versus MonomialList@#? – Mr.Wizard Aug 03 '13 at 05:50
  • @Mr.Wizard MonomialList is the right choice, I think. But using Sort seems like a cute, original twist. – Jens Aug 03 '13 at 06:09
5

I hope there is a better way but here is something to build upon:

TraditionalForm @ Row[MonomialList@#, "+"] & /@
  {x^2 + x + 5, -x^2 + x + 5, x^2 + x, -x^2 + x}

Mathematica graphics

Jens pointed out a bug in my original method. Here's another:

HoldForm[+##] & @@ MonomialList@# & /@
 {x^2 + x + 5, -x^2 + x + 5, x^2 + x, -x^2 + x, -x^2 - x}

enter image description here

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • 2
    Similar Row[MonomialList[-x^2 + x, {x}, "DegreeLexicographic"], "+"] – ssch Mar 06 '13 at 00:06
  • Is it the case that Plus@@MonomialList[expr] == expr for any expression? If so, then I can define a format: Format[xPlus[x___]] := Row[Riffle[{expr}, "+"]] and then xPlus := Plus and then use HoldForm[xPlus@@MonomialList[expr]] to the display ordering that I want while still having a valid expression when the hold is released (because the xPlus will be changed to Plus). – RandomBits Mar 06 '13 at 03:47
  • 1
    After I upvoted this, I realized it's not quite right: Try TraditionalForm@Row[MonomialList@#, "+"] &[-x^2 - x] and you get $-x^2+,-,x$. The same error happens with the solution by @ssch. – Jens Aug 03 '13 at 05:16
  • @Jens Okay, maybe a hybrid of the two answers will work. Let me try some stuff. – Mr.Wizard Aug 03 '13 at 05:25
1
poly[x_] := 
 Block[{Plus}, 
  x // Sort // Reverse // Evaluate // HoldForm // TraditionalForm]
poly[x - x^2]
(* -x^2+x *)
poly[-x^2 + x]
(* -x^2+x *)
VF1
  • 4,702
  • 23
  • 31
  • This is the best answer, I think (+1). But do you really need HoldFirst? – Jens Aug 03 '13 at 05:18
  • @Jens This changes the order of all the other terms, which in my understanding is not desired. I believe all but the last expression should agree with {x^2 + x + 5, -x^2 + x + 5, x^2 + x, -x^2 + x} // TraditionalForm. That is to say, it should match my answer. – Mr.Wizard Aug 03 '13 at 05:19
  • @Mr.Wizard You're right. I thought Sort on blocked Plus is a clever idea, but it doesn't quite do what's needed either. – Jens Aug 03 '13 at 05:24
  • @Jens, Mr. Wizard good catches - guess I should have done more testing. – VF1 Aug 03 '13 at 05:33
  • @Jens moreover, it fails with -x + 1. – Kuba May 23 '14 at 09:52