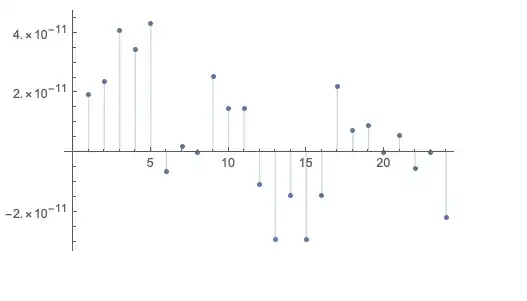
I am trying to find a model with a Fourier basis for this data:
data = {{1, -0.5}, {2, -15}, {3, 30}, {4, 184.25}, {5,
2143.75}, {6, 6234.75}, {7, 11969.75}, {8, 16940.75}, {9,
20484.75}, {10, 23084.25}, {11, 24577.25}, {12, 26321.75}, {13,
29709.25}, {14, 36357.75}, {15, 40502.25}, {16, 38244.25}, {17,
30486.25}, {18, 19492.75}, {19, 13318.25}, {20, 12267.25}, {21,
12376.25}, {22, 12375.75}, {23, 12376.25}, {24, 12376.25}};
Help is greatly appreciated thanks!