I have the following question about solving a PDE:
L = 7 (*domain size*); a=4; b=2;
d = 10.6455; e = 0.90998; (*to be adjusted*)
c = 1/10; (*small parameter in initial condition*)
sys = {D[u[x, t], t] + u[x, t]*D[u[x, t], x] - D[u[x, t], {x, 2}]
+ D[u[x, t], {x, 4}] + a*1/(2 L)*int[D[u[x, t], {x, 3}], x, t]
- d*D[u[x, t]*D[u[x, t], x], x] + b*e*D[u[x, t], {x, 3}] == 0,
u[-L, t] == u[L, t], u[x, 0] == c*Cos[(\[Pi]*x)/L]};
The method to solve the PDE is a slight modification of @Michael E2's answer. Note: to reproduce the error, please try nGrid = 31, the computation will finish in about 1100s with a singularity at t=0.478698.
periodize[data_] := Append[data, {N@L, data[[1, 2]]}];(*for periodic interpolation*)
tmax = 10; nGrid = 31(*91*);
inicos[x_] = c Cos[(\[Pi]*x)/L];
Block[{int}, int[u_, x_?NumericQ, t_ /; t == 0] := (cnt++;
NIntegrate[inicos'''[xp]*Cot[\[Pi] (x - xp)/(2*L)], {xp, x - L, x, x + L},
Method -> {"InterpolationPointsSubdivision", Method -> "PrincipalValue"},
PrecisionGoal -> 8, AccuracyGoal -> 8, MaxRecursion -> 10]);
int[uppp_?VectorQ, xv_?VectorQ, t_?NumericQ] := Function[x, cnt++;
NIntegrate[Interpolation[periodize@Transpose@{xv, uppp}, xp,
PeriodicInterpolation -> True]*Cot[\[Pi] (x - xp)/(2*L)], {xp, x - L, x, x + L},
Method -> {"InterpolationPointsSubdivision", Method -> "PrincipalValue"},
PrecisionGoal -> 8, AccuracyGoal -> 8, MaxRecursion -> 10]] /@xv;
(*monitor while integrating pde*)
Clear[foo];
cnt = 0;
PrintTemporary@Dynamic@{foo, cnt, Clock[Infinity]};
(*broken down NDSolve call*)
Internal`InheritedBlock[{MapThread},
{state} = NDSolve`ProcessEquations[sys, u, {x, -L, L}, {t, 0, tmax},
Method -> {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "MinPoints" -> nGrid, "MaxPoints" -> nGrid,
"DifferenceOrder" -> 2}(*, Method\[Rule]{"StiffnessSwitching",
"NonstiffTest"\[Rule]Automatic}*)}, AccuracyGoal -> Infinity,
(*WorkingPrecision -> 20,*) MaxSteps -> \[Infinity],
StepMonitor :> (foo = t)];
Unprotect[MapThread];
MapThread[f_, data_, 1] /; ! FreeQ[f, int] := f @@ data;
Protect[MapThread];
NDSolve`Iterate[state, {0, tmax}];
sol = NDSolve`ProcessSolutions[state]]
] // AbsoluteTiming
When solving the equation, I always got the following error:
NDSolve`Iterate::ndsz: At t == ...., step size is effectively zero; singularity or stiff system suspected.
Actually, you will see a series of warnings, such as slwcon and ncvb, which could be ignored (please see Michael's comments in the above link). In addition, I also got the warning
Warning: estimated initial error on the specified spatial grid in the direction of independent variable x exceeds prescribed error tolerance.
By increasing nGrid from 31 up to 91, the warning remains. However, I think this is not that serious.
Summary of my trial:
With
nGrid = 91as above, the singularity occurs att=0.7289. Observe the solution at the final moment.Plot[{Evaluate[u[x, 0] /. sol], Evaluate[u[x, 0.7289] /. sol]}, {x, -L, L}, PlotRange -> {{-L, L}, All}, ImageSize -> 400, PlotPoints -> 60, AspectRatio -> 0.5, Frame -> True, Axes -> False, PlotStyle -> {Black, Red}]
- With
d=10.4187,e=0.639919, andnGrid = 31(faster computation), the singularity occurs earlier att=0.5019. I plotted the solution at the final moment.
- I also tried
nGrid = 46withMethod\[Rule]{"StiffnessSwitching", "NonstiffTest"\[Rule]Automatic}, but the singularity error remains at aboutt=0.86. The solutions at the finial moment are similar to the above plots. For example, withnGrid = 46, singular timet=0.8554, the solution is as follows: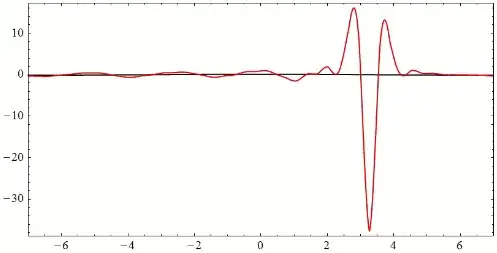
We can see that the fluctuations in the solution are concentrated in a small interval and that it doesn't seem to have developed a real singularity (since its amplitudes are still acceptable physically).
Based on this observation, to deploy as many as possible points to resolve the local solution, I tried to use a one-order smaller domain of L=0.7 with d=2.14617, e=-9.20831. Now NDSolve can run up to tmax = 50 without singularity using either nGrid = 46 or 31. But the solution is always a straight line close to zero, which I don't know why.
The question:
I understand that the PDE might have a singularity for some values of the parameters. I also found that the term - d*D[u[x, t]*D[u[x, t], x], x] should be the reason for the singularity because when this term is removed this equation can be solved.
I just try to find somehow a well-behaved solution, which can develop up to a large time, say, tmax=50, with a proper set of parameters' values. I prefer to adjust firstly L, d and e. Please give me some suggestions on how to adjust the parameters and/or correct the code to avoid the singularity. Thank you for your time.
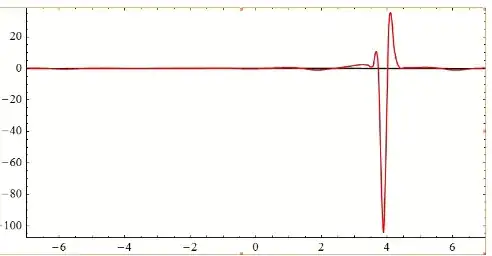



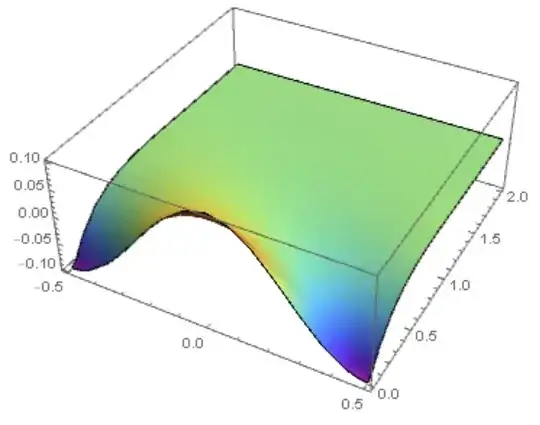

int = 0, we get a smooth solution. This smooth solution should be used in computingint, as in my answer. Then we get a slight change in the smooth solution. But direct use ofintproduces numerical instability (it can be easily proved). – Alex Trounev Oct 31 '19 at 11:49