How to use only Neumann boundary conditions and a normalization constraint on a PDE

Question

I'm trying to solve the stationary PDE

c = {{5, 0}, {0, 5}};
alpha = {x - 50, y - 50};
pde = Div[-c.Grad[u[x, y], {x, y}] - alpha*u[x, y], {x, y}];

(following the naming convention from https://reference.wolfram.com/language/FEMDocumentation/tutorial/SolvingPDEwithFEM.html)

with zero-flux (Neumann zero) boundary conditions. It is clear to me that the solution is not unique until additional boundary conditions of Dirichlet-type are specified. However I'd rather want to apply a normalization constraint to the solution:

$\int\limits_{0}^L\int\limits_{0}^L u(x,y) dx dy = 1$

I've already found a similar question regarding a one-dimensional problem: Imposing boundary condition and normalization on an ODE which I've tried to adapt for my 2-dimensional system:

sol = NDSolveValue[{pde == NeumannValue[0, True], 
D[U[x, y], x, y] == u[x, y], 
DirichletCondition[U[x, y] == 1, x == L && y == L]}, 
{u, U}, {x, 0, L}, {y, 0, L}]

However Mathematica says

NDSolveValue::femibcnd: No DirichletCondition or Robin-type NeumannValue was specified for {u}; the result may not be unique.

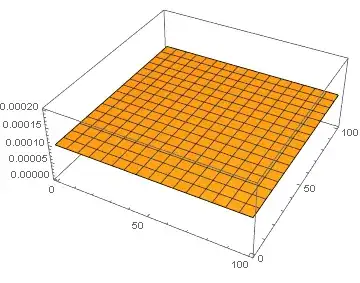
and the solutions to u and its antiderivative U look rather messed up:

which is definelty wrong, as the integral over u(x,y) is not equal to one. How do I properly impose a normalization constraint like that onto my solution?

Strongly related: https://mathematica.stackexchange.com/q/191476/1871 — xzczd, Oct 28 '19 at 05:11

score 5 · Accepted Answer · answered Oct 27 '19 at 13:16

One approach may be to turn the problem into a transient, move your fluxes to the boundary as Neumann Values, solve to a long time, and consider that the steady-state solution.

Needs["NDSolve`FEM`"];
ht = L;
len = L;
top = ht;
bot = 0;
left = 0;
right = len;
bounds = <|xl -> 1, xr -> 2, ybot -> 3, ytop -> 4|>;
regs = <|domain -> 10|>;
bmesh = ToBoundaryMesh[
   "Coordinates" -> {{left, bot}(*1*), {right, bot}(*2*), {right, 
      top}(*3*), {left, top}(*4*)}, 
   "BoundaryElements" -> {LineElement[{{1, 2}(*bottom edge*)(*1*), {4,
         1}(*left edge*)(*2*), {2, 3}(*3*), {3, 4}(*4*)}, {bounds[
        ybot], bounds[xl], bounds[xr], bounds[ytop]}]}];
bmesh["Wireframe"["MeshElementMarkerStyle" -> Blue, 
  "MeshElementStyle" -> {Green, Red, Black, Blue}, ImageSize -> Large]]
mesh = ToElementMesh[bmesh, 
   "RegionMarker" -> {{{(left + right)/2, (bot + top)/2}, 
      regs[domain], 10}}];
mesh["Wireframe"["MeshElementStyle" -> {FaceForm[Red]}, 
  ImageSize -> Large]]
nvleft = NeumannValue[50, ElementMarker == bounds[xl]];
nvright = NeumannValue[-50, ElementMarker == bounds[xr]];
nvtop = NeumannValue[50, ElementMarker == bounds[ytop]];
nvbot = NeumannValue[-50, ElementMarker == bounds[ybot]];
pde = D[u[t, x, y], t] + Div[-c.Grad[u[t, x, y], {x, y}], {x, y}] == 
   nvleft + nvright + nvtop + nvbot;
uifn = NDSolveValue[{pde, u[0, x, y] == 1/L^2}, 
   u, {t, 0, 1000}, {x, y} \[Element] mesh];
imgs = Table[
   Plot3D[uifn[t, x, y], {x, y} \[Element] mesh, 
    PlotRange -> All], {t, 0, 1000, 20}];
ListAnimate@imgs

As you can see, the integration is close to 1 at the end time.

NIntegrate[uifn[1000, x, y], {x, 0, L}, {y, 0, L}]
(* 1.00011 *)

Interestingly, I have already been using this approach. However I've always thought of it as a kind of workaround, as I was sure it should be somehow easier to solve the stationary problem directly. It is reassuring though that other people use this trick, too. I will wait a few more days to see if someone comes up with an elegant way to solve the stationary problem directly before I accept your answer. — user2483352, Oct 28 '19 at 12:43
Actually, stationary problems can be more difficult as they can have multiple steady state answers due to non-linearity and getting the right initialization can be tricky. I have used the FEM fluid solver AcuSolve quite extensively and it solved steady problems by using large timesteps. So, I often think of steady problems in FEM as transients with long steps. If I know the solution should converge to a steady-state, I often will ramp from rest conditions. It never hurts to wait for better answers. — Tim Laska, Oct 28 '19 at 16:04

How to use only Neumann boundary conditions and a normalization constraint on a PDE

1 Answers1

Linked