Geometric transform of a plot with legends and title

Question

I'm doing a ternary phase diagram, so I want to plot it in a triangle and not in a square. If I'm doing the transformation with legends it doesn't work, but if I don't put legends it does work. Why and how can I fix that please ?

Here is the first part of the code with the variables :

F[x_, phi_] = -(-1 + phi) Log[1 - phi] + phi x Log[phi x] - 
  phi (-1 + x) Log[phi - phi x]
Hxx[x_, phi_] = Simplify[D[F[x, phi], x, x]];
Hpp[x_, phi_] = Simplify[D[F[x, phi], phi, phi]];
Hpx[x_, phi_] = FullSimplify[D[F[x, phi], x, phi]];
det = Sign[
   Simplify[(Hpp[x, phi]*Hxx[x, phi] - Hpx[x, phi]^2)] /. n -> 0];
detab = Simplify[det /. x -> a/(a + b) /. phi -> a + b];

Here I'm writing the transform and the plot :

{error, xf} = 
  FindGeometricTransform[{{0, 0}, {1, 0}, {1, Tan[Pi/3]}/2}, {{0, 
     0}, {1, 0}, {0, 1}}];

{dp = Show[{DensityPlot[
     detab, {a, 10^(-3), 1 - 10^(-3)}, {b, 10^(-3), 1 - 10^(-3)}, 
     PlotLegends -> Automatic, FrameLabel -> Automatic, 
     PlotLabel -> "phase diagram", 
     RegionFunction -> Function[{a, b}, a + b < 1]], 
    ContourPlot[{a == 2* 10^(-3), b == 2*10^(-3), 
      a + b == 1 - 2*10^(-3)}, {a, 10^(-3), 1 - 10^(-3)}, {b, 10^(-3),
       1 - 10^(-3)}, ContourStyle -> Black]}],
 Graphics[GeometricTransformation[First@dp, xf]]}

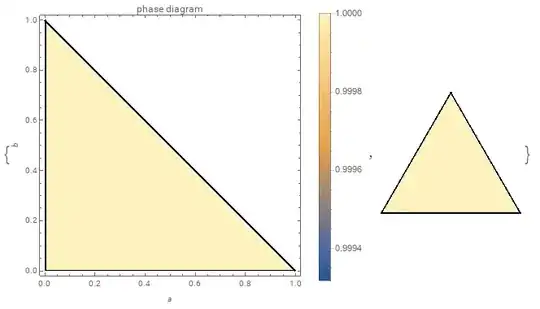
And here is what I get :

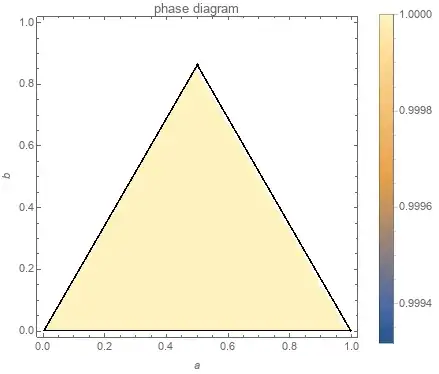
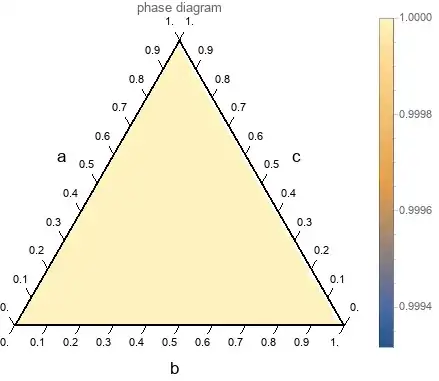
But if I'm not writing the legends and co :

{dp = Show[{DensityPlot[
     detab, {a, 10^(-3), 1 - 10^(-3)}, {b, 10^(-3), 1 - 10^(-3)},  
     RegionFunction -> Function[{a, b}, a + b < 1]], 
    ContourPlot[{a == 2* 10^(-3), b == 2*10^(-3), 
      a + b == 1 - 2*10^(-3)}, {a, 10^(-3), 1 - 10^(-3)}, {b, 10^(-3),
       1 - 10^(-3)}, ContourStyle -> Black]}],
 Graphics[GeometricTransformation[First@dp, xf]]}

kglr · Accepted Answer · 2019-10-30T04:17:46.817

Use dp[[1, 1]] instead of First @ dp in your first code block:

Quiet@{dp = Show[{DensityPlot[detab, 
      {a, 10^(-3), 1 - 10^(-3)}, {b, 10^(-3), 1 - 10^(-3)},
      PlotLegends -> Automatic, FrameLabel -> Automatic, 
      PlotLabel -> "phase diagram", 
      RegionFunction -> Function[{a, b}, a + b < 1]], 
  ContourPlot[{a == 2*10^(-3), b == 2*10^(-3), a + b == 1 - 2*10^(-3)}, 
      {a, 10^(-3), 1 - 10^(-3)}, {b, 10^(-3), 1 - 10^(-3)},
      ContourStyle -> Black]}], 
  Graphics[GeometricTransformation[dp[[1, 1]], xf]]}

"is there a way to transfer the axes and the legends/title?"

MapAt[GeometricTransformation[#, xf] &, dp, {1, 1}]

Update: Adding axes and ticks to the transformed graphics:

tl = 10;
axes = Join[{Line[{{0, #}, Offset[{-tl, tl}, {0, #}]}] ,
    Line[{{#, 0}, Offset[{0, -tl}, {#, 0}]}] ,
    Line[{{#, 1 - #}, Offset[{0, tl}, {#, 1 - #}]}]} & /@ Range[0, 1, 1/10],
  {Line[{{0, 0}, {0, 1}}], Line[{{0, 0}, {1, 0}}], Line[{{0, 1}, {1, 0}}]}];

ticklabels = {Text[Round[#, .1], Offset[xf@{-2 tl, 2 tl}, xf@{0, #}]] ,
        Text[Round[#, .1], Offset[xf@{0, -2 tl}, xf@ {#, 0}]] ,
        Text[Round[1 - #, .1], Offset[xf@{0, 2 tl}, xf@ {#, 1 - #}]]} & /@ 
       Range[0, 1, 1/10];

axislabels = MapThread[Text[Style[#, 16], Offset[xf @ #2[[1]], xf @ #2[[2]]]] &, 
   {{"a", "b",  "c"}, 
   {{{-50, 30}, {0, 1/2}}, {{20, -50}, {1/2, 0}}, {{20, 30}, {1/2, 1/2}}}}];

Legended[Graphics[{axislabels, ticklabels, 
  GeometricTransformation[{axes, dp[[1, 1]]}, xf]}, PlotLabel -> "phase diagram"],
  dp[[2]]]

Great thx ! But is there a way to transfer the axes and the legends/title ? — J.A, Oct 29 '19 at 11:25
And to put the $b$-axe along the the corresponding side of the triangle please ? — J.A, Oct 29 '19 at 11:42
@J.A, pls see the answers to How to plot ternary density plots? to get the axes, labels and ticks on the triangle sides. — kglr, Oct 29 '19 at 11:48
@J.A, please see the update re axes/ticks on the sides of the triangle. — kglr, Oct 30 '19 at 01:51

Geometric transform of a plot with legends and title

1 Answers1