Constraint of NDSolve with an integral of the solution

Question

I'd like to use NDSolve and to make a constraint with an integral.

For example, take the very simple : $$f'(x)=-f(x)/x_0 $$ the solution is $$f(x)=f_0 e^{-x/x_0} $$

And $f_0$ is given by : $$\int_0^{+\infty} f(x)dx=F\implies f_0 = F/x_0 $$

Now let's make it a bit more complicated :

$$f'(x)(1+Df(x)(1-f(x))f(x)^2) =-f(x)/x_0$$

let's assume : $D=20,x_0=1$.

One can solve this equation using boundary conditions :

f[x_] = f[x] /. 
   NDSolve[{f'[x] (1 + 20 f[x] (1 - f[x]) f[x]^2) == -f[x], 
     f[0] == 0.6}, f, {x, 0, 5}];
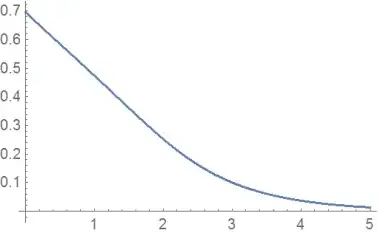
Plot[f[x], {x, 0, 5}]

But I'd like to solve it using the condition : $\int_0^5f(x)dx=1.2$ for example.

How can I do ?

What I imagined is something like that :

F = 1.2;
f[x_, a_] := 
  f[x] /. NDSolve[{f'[x] (1 + 20 f[x] (1 - f[x]) f[x]^2) == -f[x], 
      f[0] == a}, f, {x, 0, 5}][[1]];
M[a_] := (NIntegrate[f[x, a], {x, 0, 5}] - F)^2
sol = NMinimize[{M[a], 0 < a < 1}, a]

But I'm getting errors :

NDSolve::ndinnt: Initial condition a is not a number or a rectangular array of numbers.

Answer 1

Can be used ParametricNDSolveValue

F = 1.2;
sol = ParametricNDSolveValue[{f'[
       x] (1 + 20 f[x] (1 - f[x]) f[x]^2) == -f[x], f[0] == a}, 
   f, {x, 0, 5}, {a}];
M[a_?NumericQ] := (NIntegrate[sol[a][x], {x, 0, 5}] - F)^2


sol1 = NMinimize[{M[a], 0 < a < 1}, a]
(*{1.03015*10^-21, {a -> 0.69524}}*)

General view of the solution and optimal solution

{Plot[Evaluate[Table[sol[a][x], {a, 0.1, 1, .1}]], {x, 0, 5}], 
 Plot[sol[a][x] /. Last[sol1], {x, 0, 5}]}

Answer 2

Knowing f[x]==FF'[x] you can expand your ode and solve without need of additional NMinimize. Only additional constraints FF[5] == 1.5,FF[0] == 0 are necessary

erg = NDSolveValue[{FF'[x] == f[x],f'[x] (1 + 20 f[x] (1 - f[x]) f[x]^2) == -f[x], FF[5] == 1.2,FF[0] == 0}, {f, FF}, {x, 0, 5} ]
Plot[{ erg[[1]][x]} , {x, 0, 5}] 

Answer 3

I am not sure whether this is what you want.

Remove["Global`*"] // Quiet;
F = 1.2;
eq = {f'[x] (1 + 20 f[x] (1 - f[x]) f[x]^2) == -f[x], g[0] == 0, 
   g[5] == F, g'[x] == f[x]};
{gSol, fSol} = 
 NDSolveValue[eq, {g, f}, {x, 0, 5}]; {gSol, fSol} // ListLinePlot


Remove["Global`*"] // Quiet;
F = 1.2;
eq = {f'[x] (1 + 20 f[x] (1 - f[x]) f[x]^2) == -f[x], f[0] == a};
fSol = ParametricNDSolveValue[eq, f, {x, 0, 5}, {a}];
intf[a_?NumericQ] := NIntegrate[fSol[a][x], {x, 0, 5}]
NMinimize[(intf[a] - F)^2, {a, 0, 10}]

---