Plot a rotated ellipse displaced from the origin, keeping dimensions constant

Question

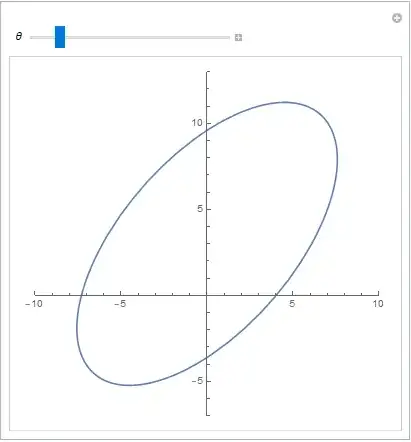
I'm trying to plot an ellipse in parametric plot, rotated by some angle and is offset from the origin with respect to the centre. I am almost there, here is my current solution

x[Rx_, Ry_, Cx_, α_, θ_] := Rx Cos[α] Cos[θ] - Ry Sin[α] Sin[θ] + Cx
y[Rx_, Ry_, Cy_, α_, θ_] := Rx Cos[α] Sin[θ] + Ry Sin[α] Cos[θ] + Cy

Manipulate[
 ParametricPlot[{x[10, 5, 0, α, θ], 
   y[10, 5, 3, α, 0.2 π]}, {α, 0, 2 π}, 
  PlotRange -> All], {θ, 0, 2 π}]

However as you will see by rotating the ellipse, when displaced by the origin, changes the effective radius parameters of the ellipse -- not what I want! I suspect that as the ellipse is rotated, the parameters $R_{x}$ and $R_{y}$ are with respect to the $x-y$ axis and not with the geometry itself, so effectively become a function of rotation.

Can anyone see a way of keeping the shape the same when rotated for any ellipse centre position? There is a solution here but the problem is if one displaces the ellipse it doesn't rotate about the centre of the ellipse, but about the origin.

score 4 · Answer 1 · answered Nov 13 '19 at 01:23

4

Why not just use a Circle and rotate with GeometricTransformation?

Manipulate[
    Graphics[
        {
        GeometricTransformation[
            Circle[{0,3}, {10,5}],
            RotationTransform[a, {0,3}]
        ]
        },
        Axes->True,
        PlotRange->{{-10,10}, {-7, 13}}
    ],
    {a, 0, 2Pi}
]

answered Nov 13 '19 at 01:23

Carl Woll

130,679
6
243
355

This is a pretty nice alternative, thanks! I give the answer to JM as while yours is a perfectly good alternative, JM answers the question completely. – user27119 Nov 13 '19 at 10:28

score 1 · Accepted Answer · answered Nov 13 '19 at 04:34

There is a solution here but the problem is if one displaces the ellipse it doesn't rotate about the centre of the ellipse, but about the origin.

It isn't overly difficult to modify rhermans's method in the question you linked to. Using Carl's example:

Manipulate[ParametricPlot[
           Composition[TranslationTransform[{0, 3}], RotationTransform[θ]][
           {10 Cos[t], 5 Sin[t]}], {t, 0, 2 π},
           PlotRange -> {{-10, 10}, {-7, 13}}], {θ, 0, 2 π}]

Manipulate

That'll do it. I wasn't aware of TranslationTransform. Thanks — user27119, Nov 13 '19 at 10:31

Plot a rotated ellipse displaced from the origin, keeping dimensions constant

2 Answers2