How can I put a moving red dot in the animated plot

Question

ss1 = NDSolve[{
  x'[t] == 8*(1 - (x[t]^2 + y[t]^2))*x[t] + ω[t]*y[t] + 1.1*Sin[11*t], 
  y'[t] == 8*(1 - (x[t]^2 + y[t]^2))*y[t] - ω[t]*x[t],
  ω'[t] == 1.1*Sin[11*t]*y[t]/(Sqrt[x[t]^2 + y[t]^2]),
  x[0] == 1, y[0] == 0, ω[0] == 2},
  {x, y, ω}, {t, 0, 200*Pi}
];

Animate[
  ParametricPlot3D[
    Evaluate[{x[t], y[t], t} /. ss1],
    {t, tmax - 2, tmax}, 
    PlotRange -> All, PlotStyle -> {Thick, Green}, 
    BoxRatios -> {1, 1, 2}, PerformanceGoal -> "Quality"
  ],
  {tmax, 2, 200*Pi}
];

When you run this in Mathematica, you will see that a trajectory is shown with specific amount of time, right now, what I am trying to do is to add a red dot on the head of this snake-like trajectory, then it will be very clear in which direction it is evolving. any help from any one will be very helpful.

kglr · Accepted Answer · 2019-11-14T20:47:45.497

2

You can use ParametricPlot3D with the options MeshFunctions, Mesh, MeshStyle and Method as follows:

Animate[ParametricPlot3D[Evaluate[{x[t], y[t], t} /. ss1], {t, tmax - 2, tmax}, 
   PlotStyle -> Directive[Thick, Green], 
   BoxRatios -> {1, 1, 2}, 
   MeshFunctions -> {#4 &}, 
   Mesh -> {{tmax}}, 
   MeshStyle -> Directive[PointSize[Large], Red], 
   PerformanceGoal -> "Quality", 
   Method -> {"BoundaryOffset" -> False}, 
   PlotRange -> {{-1.2, 1.2}, {-1.2, 1.2}, All}, 
   ImagePadding -> 30] /. Point -> (Scale[Sphere[#, .05], {1, 1, .5}] &), 
{tmax, 2, 200*Pi}, 
 AnimationRate -> 1/500]

edited Nov 14 '19 at 20:47

answered Nov 14 '19 at 01:16

kglr

394,356
18
477
896

It is very nice of you, I will give it a try, therefore, in that case, if I use the ParametricPlot(2D case), will it also work the same way as the 3D plot?? – xiaofu li Nov 14 '19 at 16:49
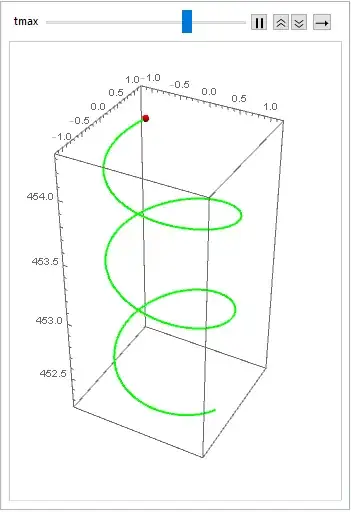
@xiaofuli, with appropriate changes (e.g.,you need to change #4& to #3& in MeshFunctions and remove BoxRatios ->... and /. Point -> ...) it should work for the 2D case. Thank you for the accept. – kglr Nov 14 '19 at 20:47
Thanks so much for the help, It works exactly the way I want. – xiaofu li Nov 15 '19 at 03:44

score 1 · Answer 2 · answered Nov 14 '19 at 00:20

1

Animate[
  Show[
    ParametricPlot3D[
      Evaluate[{x[t], y[t], t} /. ss1], {t, tmax - 2, tmax},
      PlotStyle -> {Thick, Green},
      BoxRatios -> {1, 1, 2}, 
      PerformanceGoal -> "Quality"
    ], 
    Graphics3D[
      {PointSize[.03], Red, Point@{x[tmax], y[tmax], tmax} /. ss1}
    ]
  ],
  {tmax, 2, 200*Pi}, 
  DefaultDuration -> 200 π
]

answered Nov 14 '19 at 00:20

NonDairyNeutrino

7,810
1
14
29

Thank you so much for the help, I will definitely give it a try with your method. – xiaofu li Nov 14 '19 at 16:50
I gave it a try with the method you showed above, it works very well. thanks again for the help. – xiaofu li Nov 15 '19 at 03:45

How can I put a moving red dot in the animated plot

2 Answers2