Showing a point on a plot as a circle rather than a disk

Question

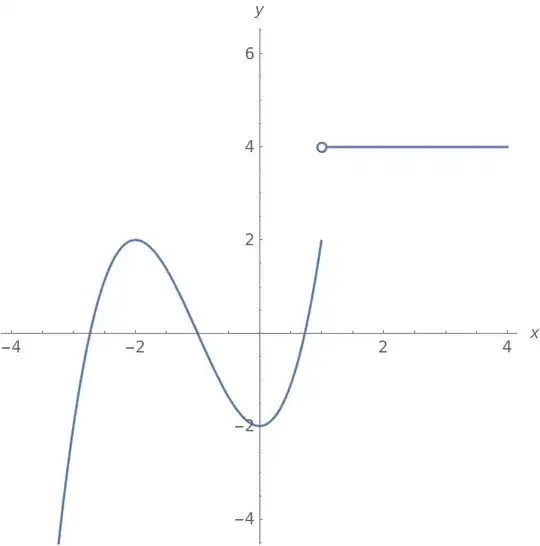
Consider the following code:

f[x_] = Which[x <= 1, x^3 + 3 x^2 - 2, x > 1, 4]

Show[
  Plot[f[x], {x, -4, 4}],
  ListPlot[{{1, f[1]}}], 
  PlotRange -> {{-4, 4}, {-4, 6}}, 
  AspectRatio -> 1,
  AxesLabel -> {x, y}, 
  Epilog -> {PointSize[0.02], Point[{{1, f[1]}}]}]

I get a plot of the discontinuous function $f(x)$.

I would like to ask you if there is a way to show the point of discontinuity on the plot of f, without it being displayed as a black disk. I would like it displayed as a circle.

A related thread. – J. M.'s missing motivation Nov 17 '19 at 10:27 — J. M.'s missing motivation, Nov 17 '19 at 10:27

score 10 · Accepted Answer · answered Nov 17 '19 at 05:45

10

I recommend plotting the function like this:

f[x_] = Which[x <= 1, x^3 + 3 x^2 - 2, x > 1, 4]

Show[Plot[f[x], {x, -4, 4}], 
 ListPlot[{{1, Limit[f[x], x -> 1, Direction -> "FromAbove"]}}, 
  PlotMarkers -> "OpenMarkers"], 
 PlotRange -> {{-4, 4}, {-4, 6}},
 AspectRatio -> 1, AxesLabel -> {x, y}]

The open marker signifies the left end point is not plotted on the second interval. The Limit function is used to calculate the point.

answered Nov 17 '19 at 05:45

LouisB

12,528
1
21
31

1

+1 I like the plot marker more than using the disk, so removing my answer. – Nasser Nov 17 '19 at 05:53
2

@LouisB's code is elegant and plots the function correctly, but in your original plot the point is highlighted when x == 1. If you want an open circle at that location, just change the limit direction to "FromBelow". – Lee Nov 17 '19 at 16:14
Thanks a lot for your answer, but when I copy and paste your code on the notebook, only the empty circle appears.... and the graph of $f$. What is wrong there? – dmtri Nov 18 '19 at 03:08
1

@dmtri My first thought is you should start with a new notebook and a fresh kernel, or Clear your variables. Can you be more explicit about what is missing? Maybe edit your question and add a new paragraph with your latest code and and a picture of the graph. – LouisB Nov 18 '19 at 03:25

score 3 · Answer 2 · edited Nov 17 '19 at 21:04

Here's how to do it using the Disk graphics primitive. It is similar to Nasser's deleted answer, but with the difference that I use ColorData[97] to make the color of the marker match the curve, and I use Offset to fix the aspect ratio issue. (No matter what aspect ratio you're using, the disk will stay circular.)

f[x_] := Which[x <= 1, x^3 + 3 x^2 - 2, x > 1, 4]

Plot[
 f[x], {x, -4, 4},
 PlotRange -> {{-4, 4}, {-4, 6}},
 AspectRatio -> 1/GoldenRatio,
 AxesLabel -> {x, y},
 Epilog -> {
   EdgeForm[{Thick, ColorData[97, 1]}], FaceForm[White],
   Disk[{1, f[1]}, Offset[{4, 4}]]
   }
 ]

Mathematica graphics

Showing a point on a plot as a circle rather than a disk

2 Answers2