0

I am trying to solve a heat conduction equation in Mathematica 9. While I can get NDSolve to work in some conditions it appears to arbitrarily fail if parameters are modified even slightly. Eventually the equation here will be expanded to multiple connected media (which I expect will cause even more instabilities). The example below is a minimal functional case.

ClearAll["Global`*"]
(*Water*)
v = -0.000001; (*Velocity (of the medium)*)
DT = 0.000000143; (*Thermal Diffusivity (k/(rho*c) *)
rho = 1000; (*Density*)
c = 4200; (*Specific Heat*)
eta = 0.001002; (*Shear Viscosity*)
Heat1D = D[u[r, t], t] + v *D[u[r, t], r] == (DT/r^2)*D[r^2*D[u[r, t], r], r] + (12*eta)/(rho*c)*(v/r)^2
NDSolve[{Heat1D, u[r, 0] == r^20*300, u[1, t] == 300}, u, {r,0.000001, 1}, {t, 0.000001, 650000}]
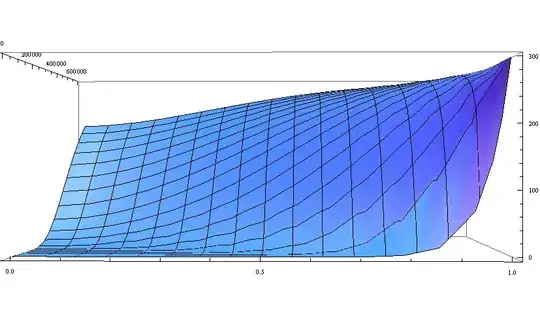
Plot3D[Evaluate[First[u[r, t] /. %]], {r, 0.000001, 1}, {t, 0.000001,600000}]

enter image description here

Which seems all right (I have left one of the boundaries unfixed).

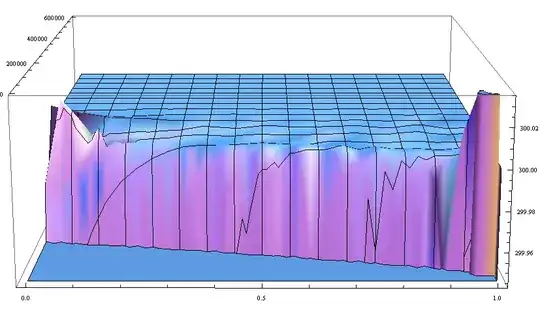
But if I make tiny changes to input variables or solver commands NDSolve blows up. i.e. change v to -0.00001 from -0.000001 gives enter image description here

Commands like MaxStepSize-> 0.1 also cause numerical issues. How would I tune NDSolve to be better behaved?

I will be coupling several equation like these together and then performing a change of variables so I have limited agency in reformatting.

EDIT: Adding boundary conditions 

u[0.5, t] == 0

to move away from 0 and considering only the interval 0.5 to 1 does not change anything. Choosing various other value for stepsize changes nothing.

I am tired
  • 113
  • 5
  • 2
    There is a 1/r in the convection term (i.e., sonething like D[u[r,t],r]/r). That probably makes the problem convection dominated since 1/r is unbounded. Also MaxStepSize-> 0.1 might be very large, inparticular because you have a unbounded convection. This all tells me that you formulated your actual problem in a very unfavorable way. Contrary what people told you, polar coordinates are very, very unsuited, in particular for FEM. – Henrik Schumacher Nov 21 '19 at 17:12
  • “I have left one of the boundaries unfixed” You should not. Please notice the bcart warning is a serious problem, for more information check the following post: https://mathematica.stackexchange.com/q/73961/1871 – xzczd Nov 22 '19 at 07:36

0 Answers0