Gaussian elimination for a Hilbert matrix

Question

I have been asked to write the Mathematica code to solve a 25x25 Hilbert matrix. The built-in function LinearSolve would not work.

I started my solution by coding a classical Gaussian elimination:

m = 25;
HM1[n_] := Table[1/(i + j - 1), {i, n}, {j, n}];
a = HM[m];
b = Table[Random[],{m}];
A = MapThread[Append,{a,b}];
Table[
  f = A[[i, j]]/A[[j, j]]; A[[i]] = A[[i]] - A[[j]]*f, 
  {j, 1, m - 1}, {i, j + 1, m}];
S = Array[0 &, m]
Table[
  A[[i, m + 1]] = A[[i, m + 1]] - Sum[A[[i, j]]*S[[j]], {j, i, m}]; 
  S[[i]] = A[[i, m + 1]]/A[[i, i]], 
  {i, m, 1, -1}];

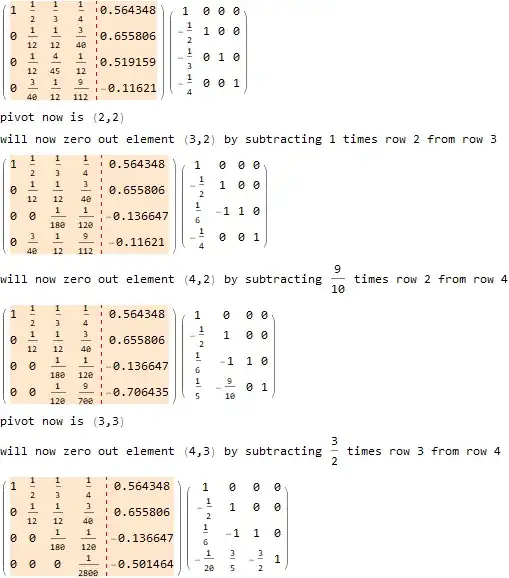
However, I am totally lost in doing the partial pivoting for the matrix. Any help?

Answer 1

I have been asked to write down a Mathematica Code

You could try displayRREF ? The latest version is at Find Elementary Matrices that produce RREF

CurrentValue[$FrontEnd, {"PrintAction"}] = {"PrintToNotebook"}
m = 4;
mat = HilbertMatrix[m];
b = Table[Random[], {m}]
displayRREF[mat, b]

Compare to Mathematica:

LinearSolve[mat, b]

Inverse[mat] // MatrixForm