I want to plot the complex sequence of numbers $(1/(1 + I))^n$ so that I can roughly see divergence/convergence. I tried DiscretePlot but doesn't seem to work.
Asked
Active
Viewed 465 times
1
-
1There are many ways to do this. One example is plotting-complex-numbers – Nasser Nov 29 '19 at 09:43
-
4Write the complex sequence in polar form: $$1/\exp{( n * i * \pi / 4 )} / \sqrt{ 2 }^n ,,.$$ The sequence spirals around and approaches zero. – LouisB Nov 29 '19 at 10:12
2 Answers
5
You can use the new in M12 function ComplexListPlot:
ComplexListPlot[Table[(1/(1+I))^n, {n, 10}]]
In earlier versions you can use ListPlot:
ListPlot[Table[ReIm[1/(1+I)^n], {n, 10}]]
If you want a continuous curve, you can use ParametricPlot:
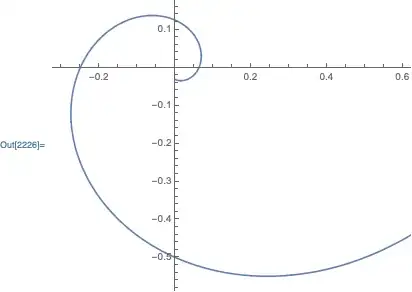
ParametricPlot[ReIm[1/(1+I)^n], {n, 0, 10}]
Carl Woll
- 130,679
- 6
- 243
- 355
2
I would be tempted to plot this in magnitude and phase:
c = Table[(1/(1 + I))^n, {n, 25}];
ListPlot[{Abs[c], Arg[c]}]
You can see the convergence of the magnitude to zero and the phase constantly decreasing with constant slope.
bill s
- 68,936
- 4
- 101
- 191