4

I am dealing with a complicated equation,involving trigonometric expressions, and I would like to solve it numerically (I gave up trying to obtain a closed form solution).

The equation:

NSolve[f[x] == 1, x]

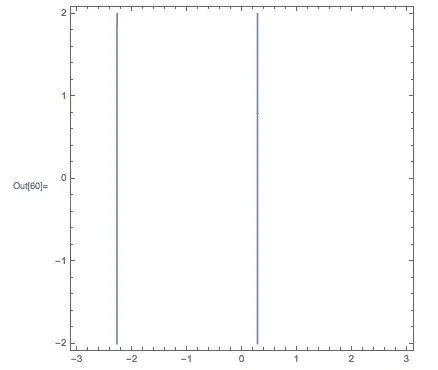
Nevertheless, NSolve seems not being able to find a solution, it runs endlessly. However, using ContourPlot, I can obtain a graph of the existing solutions within a few seconds:

ContourPlot[f[x]== 1, {x, -3, 3}, {y, -2, 2}]

enter image description here

My question is, how can I extract these solutions from the ContourPlot? or, is there a quick way to obtain these solutions ? (at least as quick as using a ContourPlot...)

It must be a common question, however I have not seen it yet. So if it turns out it is a duplicate please let me know and I will delete my question.

Any remark or observation is always appreciated, thanks.

EDIT:

For completeness, I add my function $f(x)$, although it is very messy and lengthy..

f[x_]:= -((3 (-43 - 48 x - 18 x^2 + 
        2 Sqrt[3] (3 + 2 x) Sqrt[8 + 6 x + 3 x^2]
          Cos[1/3 Arg[
            10 + 2 x - 12 x^2 - 4 x^3 + (
             2 I Sqrt[
              1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
             3 Sqrt[3])]] + (8 + 6 x + 3 x^2) Cos[
          2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
             2 I Sqrt[
              1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
             3 Sqrt[3])]] - 
        18 Sqrt[8 + 6 x + 3 x^2]
          Sin[1/3 Arg[
            10 + 2 x - 12 x^2 - 4 x^3 + (
             2 I Sqrt[
              1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
             3 Sqrt[3])]] - 
        12 x Sqrt[8 + 6 x + 3 x^2]
          Sin[1/3 Arg[
            10 + 2 x - 12 x^2 - 4 x^3 + (
             2 I Sqrt[
              1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
             3 Sqrt[3])]] + 
        8 Sqrt[3]
          Sin[2/3 Arg[
            10 + 2 x - 12 x^2 - 4 x^3 + (
             2 I Sqrt[
              1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
             3 Sqrt[3])]] + 
        6 Sqrt[3]
          x Sin[2/
           3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
             2 I Sqrt[
              1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
             3 Sqrt[3])]] + 
        3 Sqrt[3]
          x^2 Sin[
          2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (

             2 I Sqrt[
              1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
             3 Sqrt[3])]]))/(3705 + 7920 x + 7164 x^2 + 3240 x^3 + 
      630 x^4 - 
      12 Sqrt[3] Sqrt[
       8 + 6 x + 3 x^2] (51 + 88 x + 57 x^2 + 14 x^3) Cos[
        1/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      2 (776 + 1542 x + 1347 x^2 + 612 x^3 + 126 x^4) Cos[
        2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      192 Sqrt[3] Sqrt[8 + 6 x + 3 x^2]
        Cos[Arg[
         10 + 2 x - 12 x^2 - 4 x^3 + (
          2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
          3 Sqrt[3])]] + 
      272 Sqrt[3] x Sqrt[8 + 6 x + 3 x^2]
        Cos[Arg[
         10 + 2 x - 12 x^2 - 4 x^3 + (
          2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
          3 Sqrt[3])]] + 
      168 Sqrt[3] x^2 Sqrt[8 + 6 x + 3 x^2]
        Cos[Arg[
         10 + 2 x - 12 x^2 - 4 x^3 + (
          2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
          3 Sqrt[3])]] + 
      48 Sqrt[3] x^3 Sqrt[8 + 6 x + 3 x^2]
        Cos[Arg[
         10 + 2 x - 12 x^2 - 4 x^3 + (
          2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
          3 Sqrt[3])]] - 
      64 Cos[4/
         3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      96 x Cos[
        4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      84 x^2 Cos[
        4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      36 x^3 Cos[
        4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      9 x^4 Cos[
        4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      1836 Sqrt[8 + 6 x + 3 x^2]
        Sin[1/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      3168 x Sqrt[8 + 6 x + 3 x^2]
        Sin[1/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      2052 x^2 Sqrt[8 + 6 x + 3 x^2]
        Sin[1/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      504 x^3 Sqrt[8 + 6 x + 3 x^2]
        Sin[1/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      1552 Sqrt[3]
        Sin[2/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      3084 Sqrt[3]
        x Sin[2/
         3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      2694 Sqrt[3]
        x^2 Sin[
        2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      1224 Sqrt[3]
        x^3 Sin[
        2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      252 Sqrt[3]
        x^4 Sin[
        2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      64 Sqrt[3]
        Sin[4/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      96 Sqrt[3]
        x Sin[4/
         3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      84 Sqrt[3]
        x^2 Sin[
        4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      36 Sqrt[3]
        x^3 Sin[
        4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      9 Sqrt[3]
        x^4 Sin[
        4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]])) - (3 (-19 - 24 x - 18 x^2 + 
      2 Sqrt[3] (1 + 2 x) Sqrt[8 + 6 x + 3 x^2]
        Cos[1/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + (8 + 6 x + 3 x^2) Cos[
        2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      6 Sqrt[8 + 6 x + 3 x^2]
        Sin[1/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] - 
      12 x Sqrt[8 + 6 x + 3 x^2]
        Sin[1/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      8 Sqrt[3]
        Sin[2/3 Arg[
          10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      6 Sqrt[3]
        x Sin[2/
         3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]] + 
      3 Sqrt[3]
        x^2 Sin[
        2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
           2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
           3 Sqrt[3])]]))/(681 + 2016 x + 2844 x^2 + 1800 x^3 + 
    630 x^4 - 
    12 Sqrt[3] Sqrt[
     8 + 6 x + 3 x^2] (9 + 28 x + 27 x^2 + 14 x^3) Cos[
      1/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    2 (200 + 534 x + 699 x^2 + 396 x^3 + 126 x^4) Cos[
      2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    64 Sqrt[3] Sqrt[8 + 6 x + 3 x^2]
      Cos[Arg[
       10 + 2 x - 12 x^2 - 4 x^3 + (
        2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
        3 Sqrt[3])]] + 
    176 Sqrt[3] x Sqrt[8 + 6 x + 3 x^2]
      Cos[Arg[
       10 + 2 x - 12 x^2 - 4 x^3 + (
        2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
        3 Sqrt[3])]] + 
    120 Sqrt[3] x^2 Sqrt[8 + 6 x + 3 x^2]
      Cos[Arg[
       10 + 2 x - 12 x^2 - 4 x^3 + (
        2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
        3 Sqrt[3])]] + 
    48 Sqrt[3] x^3 Sqrt[8 + 6 x + 3 x^2]
      Cos[Arg[
       10 + 2 x - 12 x^2 - 4 x^3 + (
        2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
        3 Sqrt[3])]] - 
    64 Cos[4/
       3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    96 x Cos[
      4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    84 x^2 Cos[
      4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    36 x^3 Cos[
      4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    9 x^4 Cos[
      4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    324 Sqrt[8 + 6 x + 3 x^2]
      Sin[1/3 Arg[
        10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    1008 x Sqrt[8 + 6 x + 3 x^2]
      Sin[1/3 Arg[
        10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    972 x^2 Sqrt[8 + 6 x + 3 x^2]
      Sin[1/3 Arg[
        10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    504 x^3 Sqrt[8 + 6 x + 3 x^2]
      Sin[1/3 Arg[
        10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    400 Sqrt[3]
      Sin[2/3 Arg[
        10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    1068 Sqrt[3]
      x Sin[2/
       3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    1398 Sqrt[3]
      x^2 Sin[
      2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    792 Sqrt[3]
      x^3 Sin[
      2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] - 
    252 Sqrt[3]
      x^4 Sin[
      2/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    64 Sqrt[3]
      Sin[4/3 Arg[
        10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    96 Sqrt[3]
      x Sin[4/
       3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    84 Sqrt[3]
      x^2 Sin[
      4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    36 Sqrt[3]
      x^3 Sin[
      4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]] + 
    9 Sqrt[3]
      x^4 Sin[
      4/3 Arg[10 + 2 x - 12 x^2 - 4 x^3 + (
         2 I Sqrt[1373 + 4338 x + 7353 x^2 + 5184 x^3 + 1296 x^4])/(
         3 Sqrt[3])]])
Ulysse
  • 93
  • 4

3 Answers3

6

Here is one possibility:

Cases[
    Normal @ Plot[f[x], {x,-3,1}, MeshFunctions->{#2&}, Mesh->{{1.}}],
    _Point,
    Infinity
]

{Point[{-2.27699, 1.}], Point[{0.276743, 1.}]}

Carl Woll
  • 130,679
  • 6
  • 243
  • 355
6

Using your definition of f[x]

ParametricPlot[{{x, f[x]}, {x, 1}}, {x, -3, 3}, WorkingPrecision -> 20]

enter image description here

Use FindRoot

sol = FindRoot[f[x] == 1, {x, #}, WorkingPrecision -> 20] & /@ {-2.5`20, 
   0.5`20}

(* {{x -> -2.2766457052790766098}, {x -> 0.27664570527907660980}} *)

Verifying,

f[x] /. sol

(* {1.00000000000000, 1.00000000000000000} *)
Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • This is a nice way, it would also allow a better precision compared to extracting it from a plot? – Ulysse Nov 29 '19 at 21:30
5

Adapted from this answer by Adam Strzebonski, it basically does under the hood what Carl Woll does and polishes the result with FindRoot, using an undocumented function:

nsol[f_, {x_, a_, b_}] := Module[{pf, cand, rts},
  pf = Evaluate[f /. x -> #] &;
  Reduce`AnalyticRootIsolation;
  cand = System`TRootsDump`GuessRealRoots[pf, {a, b}];
  rts = Quiet[x /. (FindRoot[f, {x, #}] & /@ cand)];
  rts = Select[rts, Chop[pf[#]] == 0 && a <= # <= b &];
  Union[rts, SameTest -> (Chop[#1 - #2] == 0 &)]]

nsol[f[x] - 1, {x, -3, 3}]
(*  {-2.27665, 0.276646}  *)
Michael E2
  • 235,386
  • 17
  • 334
  • 747