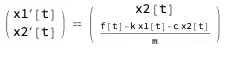Is there a built-in function that expresses a 2nd order ODE as 1st order ODE's? If not, how can one decouple a 2nd ODE to a first-order one using Mathematica?
I couldn't find it here: Why is NDSolve solving in term of two 1st order ODE slower than 2nd order?