In this sum over $k$
Sum[Sin[k (k - 1)]/k, {k, 1, ∞}]
the result still containes the summation index $k$.
(* Out 1/2 I (Log[E^-I (E^I - E^(I k))] - Log[E^(-I k) (-E^I + E^(I k))]) *)
What is happening here?
If the sum were divergent, Mathematica would normally return the input.
Sum[1/k, {k, 1, ∞}]
(* Out[148]= $\sum _{k=1}^{\infty } \frac{1}{k}$ *)
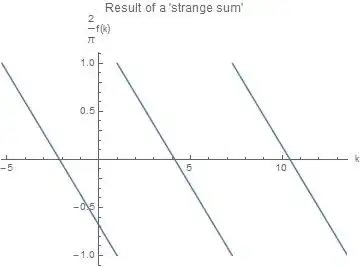
Nevertheless plotting the r.h.s. (designated by $f$) as a function of $k$
Plot[2/π f, {k, -2 π + 1, 1.1 + 6 π},
PlotLabel -> "Result of a 'strange sum'", AxesLabel -> {"k", "f(k)"},
PlotRange -> {{-2 π + 1, 4 π + 1}, All}]
we see that it is discontinuous and in the range from $-\frac{\pi}{2}$ to $\frac{\pi}{2}$.
This could be an indication the the sum is divergent delivering values in this range. I have not studied the convergence, but confined myself to the Mathematica question.
Cross reference to the convergence question: https://math.stackexchange.com/q/3466339/198592
NSumcomplains of convergence failure. I'd expect logarithmic divergence here, although I can't prove it. – John Doty Dec 06 '19 at 18:59Table[Sin[k*(k-1)]/k, {k, 10^7}] // N // Total. Maybe ask at https://math.stackexchange.com if you need the exact limit. – Roman Dec 06 '19 at 19:20Sum[Sin[k (k - 1)]/k, {k, 1, \[Infinity]}]returns the input. – user64494 Jun 08 '22 at 10:23