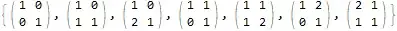4

I am trying to make a list of 2x2 matrices whose entries are all possible permutations of 0,1,2 and det=1 mod 2 arithmetic.

First I tried to create a Table like this

T1 = Table[{{i, j}, {m, n}}, {i, 0, 2}, {j, 0, 2}, {n, 0, 2},{m,0,2}]

But how to extract it as a list of matrices in MatrixForm and including the condition of determinant one?

ricci1729
  • 196
  • 1
  • 10
  • I saw that you changed the requirement for the determinant. I added that option to my answer. – MarcoB Dec 10 '19 at 16:19

3 Answers3

7
n = 2;
sol = Solve[{Mod[a d - b c, 2] == 1, 
    And @@ Thread[0 <= {a, b, c, d} <= n]}, {a, b, c, d}, Integers];

solutions = {{a, b}, {c, d}} /. sol;

Length @ solutions

16

TeXForm @ Grid[Partition[MatrixForm /@ solutions, 4]]

$\begin{array}{cccc} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right) & \left( \begin{array}{cc} 0 & 1 \\ 1 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 0 & 1 \\ 1 & 2 \\ \end{array} \right) & \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right) \\ \left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 1 & 0 \\ 2 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 1 & 1 \\ 1 & 0 \\ \end{array} \right) \\ \left( \begin{array}{cc} 1 & 1 \\ 1 & 2 \\ \end{array} \right) & \left( \begin{array}{cc} 1 & 1 \\ 2 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 1 & 2 \\ 0 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 1 & 2 \\ 1 & 1 \\ \end{array} \right) \\ \left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 2 & 1 \\ 1 & 0 \\ \end{array} \right) & \left( \begin{array}{cc} 2 & 1 \\ 1 & 1 \\ \end{array} \right) & \left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \\ \end{array} \right) \\ \end{array}$

For n = 3 we get

Length @ solutions

96

Grid[Partition[MatrixForm /@ solutions, 12]]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
6

Using your Table expression, you will want to Flatten the results to obtain a list of matrices, rather than nested lists:

t1 = Table[{{i, j}, {m, n}}, {i, 0, 2}, {j, 0, 2}, {n, 0, 2}, {m, 0, 2}]~Flatten~3;

The same thing can be obtained more directly using Tuples:

t1 = Tuples[Range[0, 2], {2, 2}]

You will then Select those matrices that have a unity determinant and apply MatrixForm to them individually using Map:

MatrixForm /@ Select[t1, Det[#] == 1 &]

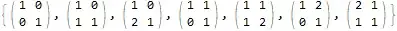
pretty-printed matrices

The question was recently changed to specify that the determinant should be 1 when considered modulo 2. This can be included as well:

MatrixForm /@ Select[t1, Mod[Det[#], 2] == 1 &]

printed matrices with modulo 2 restriction

It is worth it to add the usual caveat: MatrixForm is a formatting wrapper that pretty-prints your matrices, but it will hinder further evaluation; see Why does MatrixForm affect calculations?.

MarcoB
  • 67,153
  • 18
  • 91
  • 189
4

As long as you don't deal with big matrices or big ranges of possible integer entries, i.e. you don't have to fear combinatorial explosion, you can just brute force generate all of them, and then select the proper ones via Select:

matrices = With[{n = 2, legalmatrixentries = Range[0, 2]}, 
  Select[
    Tuples[legalmatrixentries, {n,n}], 
    OddQ @* Det (* (Mod[Det[#], k] == 1 &) for general modular arithmetic mod k *)
  ]
]
MatrixForm /@ matrices

$$ \left\{\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right),\left( \begin{array}{cc} 0 & 1 \\ 1 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 0 & 1 \\ 1 & 2 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 0 \\ 2 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 1 \\ 1 & 0 \\ \end{array} \right),\\\left( \begin{array}{cc} 1 & 1 \\ 1 & 2 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 1 \\ 2 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 2 \\ 0 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 2 \\ 1 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 2 & 1 \\ 1 & 0 \\ \end{array} \right),\left( \begin{array}{cc} 2 & 1 \\ 1 & 1 \\ \end{array} \right),\left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \\ \end{array} \right)\right\} $$

Related integer sequences:

  • Nr. of solutions for the mod2 case: A210370
  • Nr. of solutions for the non mod2 case: A171503

Updated

  • Updated answer to give solutions for modular arithmetic (mod 2)
Community
  • 1
Thies Heidecke
  • 8,814
  • 34
  • 44
  • 1
    You could give multiple dimensions to Tuples to get arrays directly, e.g. Tuples[legalmatrixentries, {n, n}], so you can avoid the Partition. – MarcoB Dec 10 '19 at 15:25
  • wrong range btw – Alucard Dec 10 '19 at 15:26
  • @MarcoB thanks for pointing that out, didn't know about it, i like! thanks! – Thies Heidecke Dec 10 '19 at 15:28
  • @Alucard The title and the code example in the OP are not matching, so i just picked the example from the title. – Thies Heidecke Dec 10 '19 at 15:28
  • Thanks a lot. Actually I did a little mistake while making the question... I wish to make the list of matrices with modular arithmetic 2 along with det one condition. I tried Modulus==2 & but it didn't work. Please let me how to incorporate the additional condition. Thanks a lot. – ricci1729 Dec 10 '19 at 15:49
  • I mean to say the det one condition is in modular arithmetic 2. – ricci1729 Dec 10 '19 at 16:09