From this answer https://mathematica.stackexchange.com/a/9773/68791 and according to the documentation:
FreeQ[list,form]test whether form occurs nowhere in list
However, I encountered some oddities:
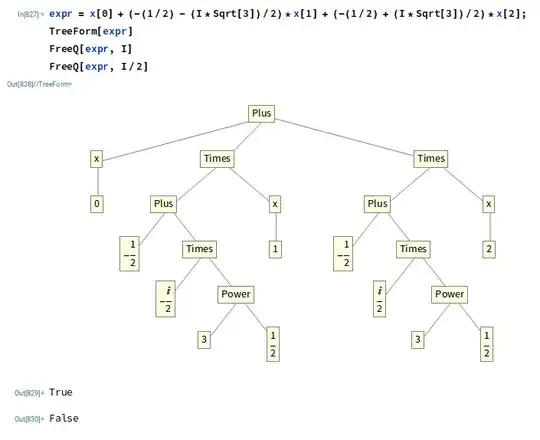
expr = x[0] + (-(1/2) - (I*Sqrt[3])/2)*x[1] + (-(1/2) + (I*Sqrt[3])/2)*x[2];
FreeQ[expr, I]
(* True -- I *is not* in expr whereas it obviously is *)
FreeQ[expr, I/2]
(* False -- I/2 *is* in expr *)
By using TreeForm it seems to me than I/2 is handled as an atom, and not as a compound expression Div[I,2].
How can I reliably test if $\large ⅈ$ (or any complex with a non-zero imaginary part) is in an expression?
ArcSin[2]? I assume it should be flagged as a nonreal, complex number. – Michael E2 Dec 13 '19 at 04:38