What can we expect from boolean region operations?

Question

In my recent efforts to design some 3D printable objects, I have been tempted to use relatively recent additions to the Wolfram Language such as RegionDifference only to be thrown into what can be best described as the Great Pit of Carkoon.

Here is one journey:

Let us start off with the simple subtraction of two objects:

RegionDifference[Region@Hexahedron[], Region@Cylinder[]]

So far so good. However, upon moving to more interesting objects, we quickly hit a brick wall.

hexpts = {{1.7, 1.5, 0}, {1.7, 10.8, 0}, {20.3, 10.8, 0}, {20.3, 1.5, 
    0}, {1.7, 1.5, 0.6}, {1.7, 10.8, 0.6}, {20.3, 10.8, 0.6}, {20.3, 
    1.5, 0.6}};
cylpts = {{14.3, 0.5, 0.6}, {14.3, 11.8, 0.6}};
cylr = 1.5;
RegionDifference[Region@Hexahedron[hexpts], 
 Region@Cylinder[cylpts, cylr]]

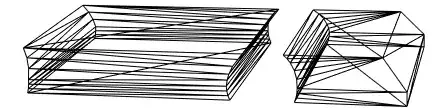
I can find no further information about this object, and subsequent operations on this region do not yield any meaningful results. Interestingly, when Rounding the Hexahedron points, functionality is restored:

Show[RegionDifference[Region@Hexahedron[Round@hexpts], 
  Region@Cylinder[cylpts, cylr]], Axes -> True]

If the problem can be solved by using only integers, then scaling the objects may serve as a workaround.

scale = 10;
Show[TransformedRegion[
  RegionDifference[Region@Hexahedron[Round@(scale hexpts)], 
   Region@Cylinder[scale cylpts, scale cylr]],
  ScalingTransform[{1, 1, 1}/scale]], Axes -> True]

I would have been satisfied with this solution, if it actually worked in a more general sense. However, it doesn't.

scale = 10;
hexpts2 = {{1.7, 1.5, 0.6}, {1.7, 10.8, 0.6}, {20.3, 10.8, 
    0.6}, {20.3, 1.5, 0.6}, {2.6, 2.1, 1.8}, {2.6, 10.2, 1.8}, {19.2, 
    10.2, 1.8}, {19.2, 2.1, 1.8}};
RegionUnion[
  Region@Hexahedron@Round@(scale hexpts),
  Region@Hexahedron@Round@(scale hexpts2)];
#[%, Cylinder[scale cylpts, scale cylr]] & /@ {RegionUnion, 
  RegionDifference}

I then came across this answer which recommends the use of BoundaryDiscretizeRegion which is encouraging, but slow.

scale = 10;
cylpts2 = {{1.7, 0.5, 0.6}, {1.7, 11.8, 0.6}};
cylr2 = 2.25;
reg1 = BoundaryDiscretizeRegion[Hexahedron@Round@(scale hexpts)];
reg2 = BoundaryDiscretizeRegion[Hexahedron@Round@(scale hexpts2)];
reg3 = BoundaryDiscretizeRegion[
   Cylinder[Round@(scale cylpts), Round@(scale cylr)]];
reg4 = BoundaryDiscretizeRegion[
   Cylinder[Round@(scale cylpts2), Round@(scale cylr2)]];

reg5 = RegionDifference[
   BoundaryDiscretizeRegion@RegionUnion[reg1, reg2],
   BoundaryDiscretizeRegion@RegionUnion[reg3, reg4]];
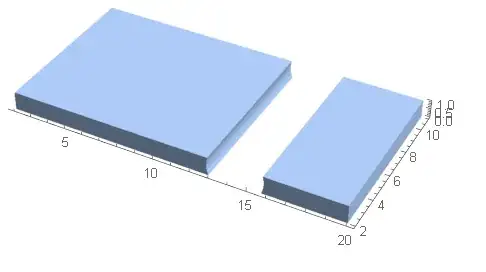
Show[TransformedRegion[reg5, ScalingTransform[{1, 1, 1}/scale]], 
 Axes -> True]

And as one can expect - since this is a question and not an answer - the workaround/hack fails when trying to scale to larger numbers in order to achieve slightly better precision in the object dimensions.

pts1 = {{1.7276, 1.47295, -0.01}, {1.7276, 10.77705, -0.01}, {20.2724,
     10.77705, -0.01}, {20.2724, 1.47295, -0.01}, {1.7276, 1.47295, 
    0.6}, {1.7276, 10.77705, 0.6}, {20.2724, 10.77705, 0.6}, {20.2724,
     1.47295, 0.6}};
pts2 = {{1.7276, 1.47295, 0.6}, {1.7276, 10.77705, 0.6}, {20.2724, 
    10.77705, 0.6}, {20.2724, 1.47295, 0.6}, {2.5802, 2.09795, 
    1.85}, {2.5802, 10.15205, 1.85}, {19.2235, 10.15205, 
    1.85}, {19.2235, 2.09795, 1.85}};
pts3 = {{1.7276, 0.47295, 0.6}, {1.7276, 11.77705, 0.6}};
pts4 = {{14.2533, 0.47295, 0.6}, {14.2533, 11.77705, 0.6}};
{cr1, cr2} = {2.25, 1.5};

scale = 100;
reg1 = BoundaryDiscretizeRegion[Hexahedron@Round@(scale pts1)];
reg2 = BoundaryDiscretizeRegion[Hexahedron@Round@(scale pts2)];
reg3 = BoundaryDiscretizeRegion[
   Cylinder[Round@(scale pts3), Round@(scale cr1)]];
reg4 = BoundaryDiscretizeRegion[
   Cylinder[Round@(scale pts3), Round@(scale cr2)]];

reg5 = RegionDifference[
   BoundaryDiscretizeRegion@RegionUnion[reg1, reg2],
   BoundaryDiscretizeRegion@RegionUnion[reg3, reg4]];
Show[TransformedRegion[reg5, ScalingTransform[{1, 1, 1}/scale]], 
 Axes -> True]

My question now is, should these operations work? Is the behavior I am observing a bug? Is it a limitation in newly implemented functionality? While recent, the functions have been around for at least 2 major releases of Mathematica, so I am making the (naive?) assumption that they are working as intended to some degree. Perhaps I am expecting too much from the software package.

Perhaps this is overly broad, but I am also interested in the extent to which we should find workarounds for these types of problems. On the one hand, the problems have existed long enough that developing solutions may prove useful. However, if Wolfram's intent is to solve these problems (eventually) then I don't know how much effort to put in to developing my own solutions.

score 6 · Accepted Answer · answered Dec 17 '19 at 17:41

When working with regions, you can either work with exact Region primitives, or discretized versions of the Region primitives. For example, a Cylinder object is an exact Region primitive, while using DiscretizeRegion on such an object produces the discretized version.

In general, using exact Region primitives inside of functions like RegionDifference is more difficult than using the discretized versions. With exact primitives, the output can't always be reduced to a single primitive, and so you're left with a BooleanRegion object. With the discretized versions, the output can always be reduced to a single discretized object. I recommend working with discretized versions.

Now, there were two issues with your first example. When working with inexact numbers, sometimes Mathematica is unable to determine whether the region is a valid region or is degenerate in some way. So:

DiscretizeRegion @ Hexahedron[hexpts]

DiscretizeRegion::regpnd: A non-degenerate region is expected at position 1 of DiscretizeRegion[Hexahedron[{{1.7,1.5,0},{1.7,10.8,0},{20.3,10.8,0},{20.3,1.5,0},{1.7,1.5,0.6},{1.7,10.8,0.6},{20.3,10.8,0.6},{20.3,1.5,0.6}}]].

DiscretizeRegion[ Hexahedron[{{1.7, 1.5, 0}, {1.7, 10.8, 0}, {20.3, 10.8, 0}, {20.3, 1.5, 0}, {1.7, 1.5, 0.6}, {1.7, 10.8, 0.6}, {20.3, 10.8, 0.6}, {20.3, 1.5, 0.6}}]]

Notice that DiscretizeRegion thinks that the Hexahedron object is degenerate. Your workaround was to use Round and scaling. It is much simpler to just rationalize the points:

DiscretizeRegion @ Hexahedron[Rationalize[hexpts, 0]]

(the other issue was minor. It is simpler to avoid using the Region wrapper, as it is mostly a wrapper that displays regions. So, use RegionDifference[Hexahedron[.], Cylinder[.]] instead of RegionDifference[Region @ Hexahedron[.], Region @ Cylinder[.]]).

All of your other examples will work fine with this approach. For instance, your last example (I fixed a typo where I think pts4 should have been used instead of pts3):

pts1 = Rationalize[{{1.7276, 1.47295, -0.01}, {1.7276, 10.77705, -0.01}, {20.2724,
 10.77705, -0.01}, {20.2724, 1.47295, -0.01}, {1.7276, 1.47295, 
0.6}, {1.7276, 10.77705, 0.6}, {20.2724, 10.77705, 0.6}, {20.2724,
 1.47295, 0.6}},0];

pts2 = Rationalize[{{1.7276, 1.47295, 0.6}, {1.7276, 10.77705, 0.6}, {20.2724, 
10.77705, 0.6}, {20.2724, 1.47295, 0.6}, {2.5802, 2.09795, 
1.85}, {2.5802, 10.15205, 1.85}, {19.2235, 10.15205, 
1.85}, {19.2235, 2.09795, 1.85}},0];

pts3 = Rationalize[{{1.7276, 0.47295, 0.6}, {1.7276, 11.77705, 0.6}}, 0];

pts4 = Rationalize[{{14.2533, 0.47295, 0.6}, {14.2533, 11.77705, 0.6}}, 0];

{cr1, cr2} = {2.25, 1.5};

reg1 = DiscretizeRegion[Hexahedron @ pts1];
reg2 = DiscretizeRegion[Hexahedron @ pts2];
reg3 = DiscretizeRegion[Cylinder[pts3, cr1]];
reg4 = DiscretizeRegion[Cylinder[pts4, cr2]];

reg5 = RegionDifference[
    RegionUnion[reg1, reg2],
    RegionUnion[reg3, reg4]
]

Very nice. I struggled with the degenerate regions, as you noticed. Is this something that I should have found in the documentation or is your grasp of the problem because you've been around the [Mathematica] block? — bobthechemist, Dec 18 '19 at 03:04
@bobthechemist, I think the fact that you have to fiddle around so much to get something to work is a bug. Sometimes you'd need to use BoundaryDiscretizeRegion sometimes DiscretizeRegion sometimes rationalized input and sometimes it is better to just use the Booleans on the symbolic (exact) region. This should be much simpler. I'd file a bug with WRI. — user21, Dec 18 '19 at 08:52

score 3 · Answer 2 · answered Mar 20 '20 at 13:19

With the new in version 12.1 OpenCascadeLink you can do boolean operations without first discretizing the sub-regions:

pts1 = {{1.7276, 1.47295, -0.01}, {1.7276, 10.77705, -0.01}, {20.2724,
     10.77705, -0.01}, {20.2724, 1.47295, -0.01}, {1.7276, 1.47295, 
    0.6}, {1.7276, 10.77705, 0.6}, {20.2724, 10.77705, 0.6}, {20.2724,
     1.47295, 0.6}};

pts2 = {{1.7276, 1.47295, 0.6}, {1.7276, 10.77705, 0.6}, {20.2724, 
    10.77705, 0.6}, {20.2724, 1.47295, 0.6}, {2.5802, 2.09795, 
    1.85}, {2.5802, 10.15205, 1.85}, {19.2235, 10.15205, 
    1.85}, {19.2235, 2.09795, 1.85}};

pts3 = {{1.7276, 0.47295, 0.6}, {1.7276, 11.77705, 0.6}};

pts4 = {{14.2533, 0.47295, 0.6}, {14.2533, 11.77705, 0.6}};

{cr1, cr2} = {2.25, 1.5};

reg1 = Hexahedron[pts1];
reg2 = Hexahedron[pts2];
reg3 = Cylinder[pts3, cr1];
reg4 = Cylinder[pts4, cr2];
reg5 = RegionDifference[RegionUnion[reg1, reg2], 
   RegionUnion[reg3, reg4]];
Needs["NDSolve`FEM`"]
Needs["OpenCascadeLink`"]
shape = OpenCascadeShape[reg5];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape];
bmesh["Wireframe"]

Looks like I need to try the upgrade. – bobthechemist Mar 20 '20 at 19:18 — bobthechemist, Mar 20 '20 at 19:18

What can we expect from boolean region operations?

2 Answers2

Linked