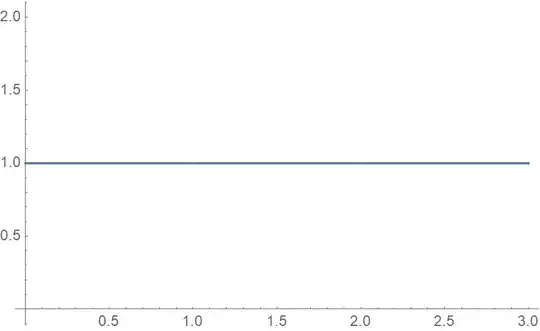
While plotting Plot[Ceiling[FractionalPart[x]], {x, 0, 3}] I noticed that the dips at integers were not being plotted. Is there a way to achieve that?
Asked
Active
Viewed 55 times
4
lineage
- 1,144
- 4
- 10
-
1Probably not. Plot[] does discrete sampling and it’s unlikely it would detect the integer values. Further it tends to exclude discontinuities, so if detected, would skip them. Look up PlotPiecewise on this site for one approach – Michael E2 Dec 21 '19 at 00:21
-
@MichaelE2 the code at https://mathematica.stackexchange.com/questions/39445/plot-a-piecewise-function-with-black-and-white-disks-marking-discontinuities/39466#39466 does the job but is mighty long. Is that the PlotPiecewise you alluded to or some in-built? – lineage Dec 21 '19 at 00:28
-
Yep, that’s it. It is long. – Michael E2 Dec 21 '19 at 00:30
1 Answers
4
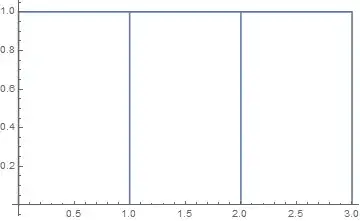
Use the options Exclusions, PlotPoints and Method as follows:
Plot[Ceiling[FractionalPart[x]], {x, 0, 3},
PlotPoints -> {30, Range[0, 3]},
Exclusions -> None,
Method -> {"BoundaryOffset" -> False}]
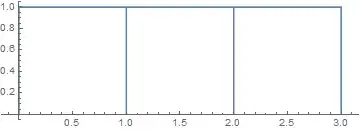
Alternatively, use ParametricPlot with the options Exclusions and PlotPoints:
ParametricPlot[{x, Ceiling[FractionalPart[x]]}, {x, 0, 3},
PlotPoints -> {30, Range[0, 3]},
Exclusions -> None]
Note the special form of the option value for PlotPoints (see see this answer by Ullrich Neumann).
kglr
- 394,356
- 18
- 477
- 896
-
1
-
3@lineage, it says sample 30 points in the domain but also include the points
{0,1,2,3}. – kglr Dec 21 '19 at 00:40 -
2@kglr that’s a really neat undocumented feature! I’d never seen it before; thank for bringing it to my attention! – MarcoB Dec 21 '19 at 05:18