Generating a certain sequence

Question

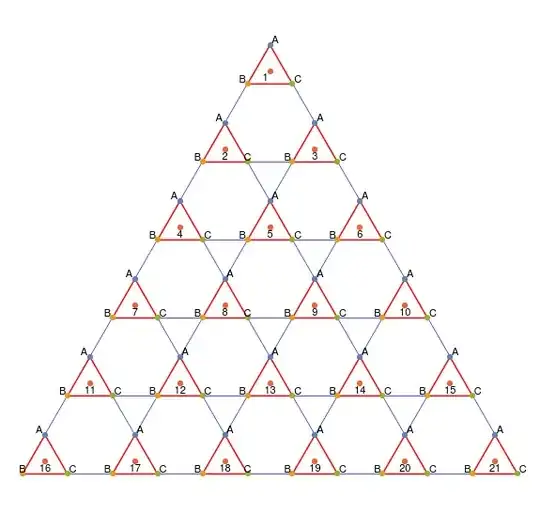
I have indexed the unit cells of the Kagome lattice. Each unit cells consists of atoms $(A,B,C)$. In this cell there are $21 \times 3$ sites.

From this picture above I see a pattern is emerging when I look at the indices of the unit cells that are connected such as

list1 = {{1}, {2, 3}, {4, 5, 6}, {7, 8, 9, 10}, {11, 12, 13, 14, 
    15}, {16, 17, 18, 19, 20, 21}}; (*connecting bases with C -> B*)

list2 = {{1, 2, 4, 7, 11, 16}, {3, 5, 8, 12, 17}, {6, 9, 13, 18}, {10,
     14, 19}, {15, 20}, {21}}; (*Connecting left edges with B -> A*)

list3 = {{1, 3, 6, 10, 15, 21}, {2, 5, 9, 14, 20}, {4, 8, 13, 19}, {7,
     12, 18}, {11, 17}, {16}}; (*Connecting right edges with C -> A*)

I have a feeling that if I start from a table Table[i,{i,1,21*3}] by performing some kind of partitioning I can achieve three of these lists. For this small system, I can write the indices, but for larger systems, it is very unlikely to have all of these lists correct. So I am trying to see the pattern to generate these list for arbitrarily large systems of $L \times 3$ sites (L is the number of total of $\bigtriangleup$ triangles)

Answer 1

lst1 = TakeList[Range @ 21, Range @ 6]

{{1}, {2, 3}, {4, 5, 6}, {7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20, 21}}

lst2 = Table[lst1[[i ;;, i]], {i, 6}]

{{1, 2, 4, 7, 11, 16}, {3, 5, 8, 12, 17}, {6, 9, 13, 18}, {10, 14, 19}, {15, 20}, {21}}

lst3 = Table[lst1[[i ;;, -i]], {i, 6}]

{{1, 3, 6, 10, 15, 21}, {2, 5, 9, 14, 20}, {4, 8, 13, 19}, {7, 12, 18}, {11, 17}, {16}}

ClearAll[threeLists]
threeLists[n_] := Module[{l = TakeList[Range[n (n + 1)/2], Range @ n]}, {l, ## & @@ 
    Table[l[[i ;;, (-1)^j  i]], {j, 0, 1}, {i, n} ]}]

threeLists[6] == {lst1, lst2, lst3}

True

threeLists[3] // Column // TeXForm

$\begin{array}{l} \{\{1\},\{2,3\},\{4,5,6\}\} \\ \{\{1,2,4\},\{3,5\},\{6\}\} \\ \{\{1,3,6\},\{2,5\},\{4\}\} \\ \end{array}$

threeLists[4] // Column // TeXForm

$\begin{array}{l} \{\{1\},\{2,3\},\{4,5,6\},\{7,8,9,10\}\} \\ \{\{1,2,4,7\},\{3,5,8\},\{6,9\},\{10\}\} \\ \{\{1,3,6,10\},\{2,5,9\},\{4,8\},\{7\}\} \\ \end{array}$

threeLists[6] // Column // TeXForm

$\begin{array}{l} \{\{1\},\{2,3\},\{4,5,6\},\{7,8,9,10\},\{11,12,13,14,15\},\{16,17,18,19,20,21\}\} \\ \{\{1,2,4,7,11,16\},\{3,5,8,12,17\},\{6,9,13,18\},\{10,14,19\},\{15,20\},\{21\}\} \\ \{\{1,3,6,10,15,21\},\{2,5,9,14,20\},\{4,8,13,19\},\{7,12,18\},\{11,17\},\{16\}\} \\ \end{array}$

An alternative formulation using NestList:

ClearAll[f, threeLists2]

f = Map[DeleteCases @ 0] @* Transpose @* PadRight;

threeLists2 = NestList[f, TakeList[Range[# (# + 1)/2], Range @ #], 2] &;

threeLists2 /@ Range[100] == threeLists /@ Range[100]

True

Answer 2

As @MarcoB suggested, looking at OEIS really did help. Then using NestList I obtained the desired result.

list1 = FoldPairList[TakeDrop, Range[21], Range[6]]

{{1}, {2, 3}, {4, 5, 6}, {7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20, 21}}

list2 = NestList[Delete[#, 1] + 1 &, Table[(i - 1) (i - 2)/2 + 1, {i, 2, 7}], 5]

{{1, 2, 4, 7, 11, 16}, {3, 5, 8, 12, 17}, {6, 9, 13, 18}, {10, 14, 19}, {15, 20}, {21}}

list3 = NestList[Delete[#, 1] - 1 &, Table[i (i + 1)/2, {i, 1, 6}], 5]

{{1, 3, 6, 10, 15, 21}, {2, 5, 9, 14, 20}, {4, 8, 13, 19}, {7, 12, 18}, {11, 17}, {16}}

Answer 3

list1

  TakeList[Range[21], Range[6]]  (*As @kglr has shown*)

{{1}, {2, 3}, {4, 5, 6}, {7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20, 21}}

list2

 TakeList[Range[21], Range[6]]//Flatten[#, {{2}}]&

{{1, 2, 4, 7, 11, 16}, {3, 5, 8, 12, 17}, {6, 9, 13, 18}, {10, 14, 19}, {15, 20}, {21}}

list3

TakeList[Range[21], Range[6]]//Flatten[#, {{2}}]&//Flatten[#, {{2}}]&

{{1, 3, 6, 10, 15, 21}, {2, 5, 9, 14, 20}, {4, 8, 13, 19}, {7, 12, 18}, {11, 17}, {16}}

Reverse/@TakeList[Range[21], Range[6]]//Flatten[#, {{2}}]&`

(Same as above)

In addition:

• The undocumented function Internal`PartitionRagged may be used instead of TakeList (as was done in original post).