When I try to solve:
Solve[y^2==441+48*x*(1+x)(-13+16*x)&&1100*10^9<=y<=1200*10^9&&x>=2,{y,x},Integers]
My code runs for 169 seconds and spits out {} which means that it didn't find any solutions. Now when I change my code to:
Solve[y^2==441+48*x*(1+x)(-13+16*x)&&1200*10^9<=y<=1400*10^9&&x>=2,{y,x},Integers]
I get the following failure (Solve::svars error):
Question: is there a way to solve for larger values of $y$ without getting that failure?
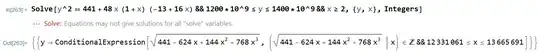
{x, 10^5, 10^9}for example. This will take a while though. – Roman Jan 07 '20 at 19:09Range[0, 1000]*10^6. I can only show you how; I cannot understand it for you. – Roman Jan 07 '20 at 21:29Range[0, 1000] 10^6 + 1and thenBlockMap[# - {0, 1} &, Range[0, 1000] 10^6 + 1, 2, 1]-- maybe look upBlockMapif you don't understand what it's doing. And then maybe execute"f" @@@ BlockMap[# - {0, 1} &, Range[0, 1000] 10^6 + 1, 2, 1]and imagine what happens when"f"is replaced bysearch. Note@@@is a form ofApply, which you can also look up if it's unfamiliar. – Michael E2 Jan 08 '20 at 04:57