0

Up until now, I have been trying to obtain an expression for an InterpolatingFunction obtained from NDSolve, by using the function Fit like this:

enter image description here

xTab = Table[{t, var[t]}, {t, 0, 2.0, 0.01}];
xFit = Fit[xTab, {1, x, x^2, x^3, x^4, x^5}, x]

giving the an expression as the following one:

0.359718 - 7.45916 x + 28.9826 x^2 - 38.8259 x^3 + 20.7638 x^4 - 
 3.81347 x^5

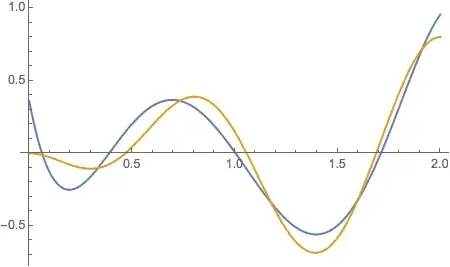
However, good approximations are dependent on the particular shape of each curve, and in this case, when we plot the original curve (blue) versus de Fit version of it (gold), we see the evident error

enter image description here

I am aware that I could add functions/terms in the Fit function like higher order polynomials or even trigonometric functions to improve the interpolation approximation, however the InterpolatingFunction at hand is (apparently) already an Hermite interpolating function of order 3:

enter image description here

How can I extract an expression for this particular InterpolatingFunction?

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
Meclassic
  • 1,005
  • 1
  • 9
  • 15
  • Assuming var was constructed with Interpolation[data], for some data, then it's a piecewise polynomial interpolation of the form in the question linked by @ChrisK. If you got it from NDSolve, the form is probably different. In all cases, it's a piecewise function with degree-3 polynomial pieces, probably a lot of pieces if you got it from NDSolve. What do you want to do with the algebraic expression? There may be better alternatives. – Michael E2 Jan 10 '20 at 18:49
  • Note that yFN = NDSolveValue[{y''[x] + x y[x] == 0, y[0] == 1, y'[0] == 0}, y, {x, 0, 2}] displays the same information as your var, but Plot[{yFN'''''[x], yFN''''''[x]}, {x, 0, 2}, PlotLegends -> "Expressions"] shows that yFN is a piecewise order-5 interpolation, not an order-3 one as its display claims. – Michael E2 Jan 10 '20 at 18:56

0 Answers0