Solving Laplace's equation in 2D using region primitives

Question

Fixed in 12.1

I was looking at examples of solving problems in electromagnetism and ran across this question, which was a great example of just that. However, looking at the Dirichlet condition, both answers define the boundary of the rectangle explicitly:

DirichletCondition[u[x, y] == 100., 
  x == 40 && 40 <= y <= 60 || 
  x == 60 && 40 <= y <= 60 || 
  40 <= x <= 60 && y == 40 || 
  40 <= x <= 60 && y == 60]

I thought to use Mathematica region capabilities to achieve the same result, and did this:

RegionBoundary @ Rectangle[{40, 40}, {60, 60}]

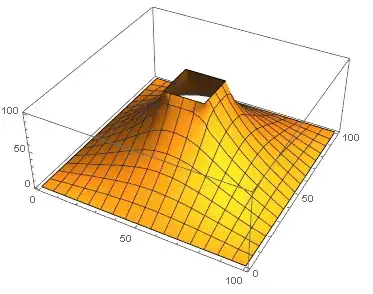
Much simpler and should be equivalent. But when I tried to solve the equation (same setup as in the linked question) it resulted in an error:

sol = 
   NDSolveValue[
     {Laplacian[V[x, y], {x, y}] == 0, 
      DirichletCondition[
        V[x, y] == 100, {x, y} ∈ RegionBoundary @ Rectangle[{40, 40}, {60, 60}]], 
        V[x, 0] == V[x, 100] == V[0, y] == V[100, y] == 0}, 
     V, 
     {x, y} ∈ 
       RegionDifference[Rectangle[{0, 0}, {100, 100}], 
       Rectangle[{40, 40}, {60, 60}]]]

No places were found on the boundary where {x,y}∈Line[{{40,40},{60,40},{60,60},{40,60},{40,40}}] was True, so DirichletCondition[V==100,{x,y}∈Line[{{40,40},{60,40},{60,60},{40,60},{40,40}}]] will effectively be ignored.

This doesn't make any sense, so I dug a little deeper. Calling RegionMember on my constructed region (FullSimplify to clean it up) gives

(x | y) ∈ Reals && 
((40 <= y <= 60 && (x == 40 || x == 60)) || (40 <= x <= 60 && (y == 40 || y == 60)))

But, if I remove the first condition

(x | y) ∈ Reals

and just copy-paste the rest in, it works (as expected, since it's the same as the explicit one given in the beginning). Just to be clear, this works:

sol = 
  NDSolveValue[
    {Laplacian[V[x, y], {x, y}] == 0, 
     DirichletCondition[
       V[x, y] == 100,  
       ((40 <= y <= 60 && (x == 40 || x == 60)) || (40 <= x <=60 && (y == 40 || y == 60)))], 
     V[x, 0] == V[x, 100] == V[0, y] == V[100, y] == 0}, 
    V, 
    {x, y} ∈ 
      RegionDifference[
        Rectangle[{0, 0}, {100, 100}], 
        Rectangle[{40, 40}, {60, 60}]]]

Thus the culprit seems to be this little bit:

(x | y) ∈ Reals

My question is: why? Both $x$ and $y$ are real numbers, so to me that little bit should only be extraneous, saying what's implied by the other conditions. Clearly this is not the case.

@user21 Oh I just added the tag, it's OP that checks it :) . — xzczd, Mar 20 '20 at 10:58

Tim Laska · Accepted Answer · 2020-01-13T16:04:43.997

8

Use a decimal point for your coordinate values so that regions are converted to real numbers.

ri = Rectangle[{40., 40.}, {60., 60.}];
rbi = Element[{x, y}, RegionBoundary@ri];
ro = Rectangle[{0., 0.}, {100., 100.}];
rdiff = RegionDifference[ro, ri];
rbo = Element[{x, y}, RegionBoundary@ro];
eqn = Laplacian[V[x, y], {x, y}] == 0;
dci = DirichletCondition[V[x, y] == 100, rbi];
dco = DirichletCondition[V[x, y] == 0, rbo];
eqns = {eqn, dci, dco};
sol = NDSolveValue[eqns, V, Element[{x, y}, rdiff]]
Plot3D[sol[x, y], Element[{x, y}, rdiff]]

edited Jan 13 '20 at 16:04

answered Jan 13 '20 at 15:17

Tim Laska

16,346
1
34
58

This works, thanks. Is there some underlying reason why using integers doesn't work or is that just a bug(-ish) of Mathematica? – imas145 Jan 13 '20 at 17:00
1

You're welcome. I would suspect that the reason is that NDSolve is calling ToElementMesh under the hood and that is compiled C or Fortran code and that an "integer" is converted to a double precision number. That double precision number may not be the same as a Mathematica Real number. – Tim Laska Jan 13 '20 at 18:59
1

@imas145, this issue seems fixed in the upcoming release. Sorry for the trouble. I think Tim's suggestion is a good workaround. – user21 Jan 14 '20 at 07:15

Solving Laplace's equation in 2D using region primitives

1 Answers1

Linked