Select variable and its derivatives

Question

A simple question:

I have this equation:

eq1=Derivative[0, 1][T1][x, t] - Derivative[1, 0][T0][x, t]^2 - 
 T0[x, t]*Derivative[2, 0][T0][x, t] - Derivative[2, 0][T1][x, t] == 0;

I want only to select terms that contain T0 or its derivatives only, that is:

-Derivative[1, 0][T0][x, t]^2 - T0[x, t]*Derivative[2, 0][T0][x, t]

Thanks in anticipation.

@MichaelE2 there is a parenthesis missing after the & symbol. Great answer though. More elegant than mine! — , Jan 15 '20 at 23:01
Yeah, I'm using Gedanken Mathematica, you know the one that's basically a keyboard without a kernel. Hard to catch those typos. — Michael E2, Jan 15 '20 at 23:09

score 2 · Answer 1 · edited Jan 16 '20 at 05:06

2

Not the most elegant solution, but you can use the Collectcommand in the following manner

eq1 =  Derivative[0, 1][T1][x, t] - 
       Derivative[1, 0][T0][x, t]^2 - 
       T0[x, t]*Derivative[2, 0][T0][x, t] - 
       Derivative[2, 0][T1][x, t]; 
       (Coefficient[#1, {T0[x, t], Derivative[1, 0][T0][x, 
       t], Derivative[1, 0][T0][x, t]^2}] & )[eq1]

This is telling you the coefficient in front of T0[x, t] and so on.

edited Jan 16 '20 at 05:06

AsukaMinato

9,758
1
14
40

answered Jan 15 '20 at 22:59

1

Could you take a look at How to copy code from Mathematica so it looks good on this site and edit your code for readability? – MarcoB Jan 15 '20 at 23:20
@MarcoB yes, that's a very good point. Thanks – Jan 16 '20 at 08:24

NonDairyNeutrino · Answer 2 · 2020-01-16T05:00:40.330

1

Block[{T1, Equal = Plus}, SetAttributes[T1, Constant]; eq1]

-Derivative[1, 0][T0][x, t]^2 - T0[x, t]*Derivative[2, 0][T0][x, t]

Or (thanks to Mr. Wizard here)

eq1 /. {s_Symbol /; StringMatchQ[SymbolName[Unevaluated@s], "T" ~~ Except["0"]] -> 0, Equal -> Plus}

-Derivative[1, 0][T0][x, t]^2 - T0[x, t]*Derivative[2, 0][T0][x, t]

edited Jan 16 '20 at 05:00

answered Jan 16 '20 at 04:15

NonDairyNeutrino

7,810
1
14
29

score 1 · Answer 3 · answered Jan 16 '20 at 04:39

While the structural operation

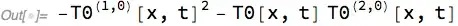
DeleteCases[eq1 /. Equal -> Subtract, _?(FreeQ[#,T0]&)]

works, I prefer using an algebraic approach on a algebraic problem.

vars = Select[Not@*FreeQ[T0]]@Variables[eq1 /. Equal -> Subtract];
coeffs = CoefficientArrays[eq1 /. Equal -> Subtract, vars];
Fold[#2 + #1.vars &, Reverse@ReplacePart[coeffs, 1 -> 0]]

Mathematica graphics

The structural approach relies on the equation being in a particular form, a flat sum of terms, which does not always happend. The algebraic approach does not. However, CoefficientArrays does rely on it being a polynomial in the variables vars.

Select variable and its derivatives

3 Answers3

Linked