(1) Pick, IntersectingQ
lis//Pick[#,MapApply[IntersectingQ,#],False]&
(* {{{a}, {b, c, d}}, {{b}, {d}}, {{a, b}, {c, d}}} *)
(2) Pick, Intersection
Syed has pointed out (in a comment) that the following does not work:
Pick[lis,Intersection@@@lis,{}]
(* Pick::incomp: Expressions {{{a}, {b, c, d}}, {{a, b}, {b, c}},
{{b, c}, {a, b, c}}, {{b}, {d}}, {{a, b}, {c, d}}} and {{}, {b}, {b, c},
{}, {}} have incompatible shapes.*)
A great explanation of how Pick works has been posted by WReach, and tracePattern defined in that post illustrates the problem very nicely:
Pick[lis,Intersection@@@lis,tracePattern[{}]]
(*
{{}, {b}, {b, c}, {}, {}} False
{} True
{b} False
Pick::incomp: Expressions {{{a}, {b, c, d}}, {{a, b}, {b, c}},
{{b, c}, {a, b, c}}, {{b}, {d}}, {{a, b}, {c, d}}} and {{}, {b},
{b, c}, {}, {}} have incompatible shapes.
*)
If at any stage, as Pick recursively scans, "the lengths of the expressions are not the same then the process is aborted with the Pick::incomp message".
Intersection@@@lis
(* {{}, {b}, {b, c}, {}, {}} *)
As {b} from the selector list does not match a pattern, the situation is reached where {b} (from sel) and {a,b} (from lis) do not have the same length, and the process aborts.
The following fails for the same reason:
Pick[lis,(MapApply[Intersection]@lis),tracePattern[_?(#==={}&)]]
(*
{{}, {b}, {b, c}, {}, {}} False
{} True
{b} False
Pick::incomp: Expressions {{{a}, {b, c, d}}, {{a, b}, {b, c}},
{{b, c}, {a, b, c}}, {{b}, {d}}, {{a, b}, {c, d}}} and {{}, {b},
{b, c}, {}, {}} have incompatible shapes.
*)
If {b} is included in the pattern given to Pick, then {{a,b}, {b,c}} from lis with be included in the list returned by Pick (this is unwanted behaviour, of course), but the "incompatible shapes" problem is circumvented (in this instance) and, as this problem does not arise in any subsequent (recursive) steps, Pick returns a result without an error message:
Pick[lis,Intersection@@@lis,tracePattern[{}| {b}]]
(*
{{}, {b}, {b, c}, {}, {}} False
{} True
{b} True
{b, c} False
b False
c False
{} True
{} True
{{{a}, {b, c, d}}, {{a, b}, {b, c}}, {}, {{b}, {d}}, {{a, b},
{c, d}}}
*)
One possible work-around
lis[[Pick[Range@Length@lis,MapApply[Intersection]@lis,{}]]]
(* {{{a}, {b, c, d}}, {{b}, {d}}, {{a, b}, {c, d}}} *)
Just for fun:
lis[[Pick[Range@Length@lis,MapApply[Intersection]@lis,
tracePattern[{}]]]]
(*
{{}, {b}, {b, c}, {}, {}} False
{} True
{b} False
{b, c} False
{} True
{} True
{{{a}, {b, c, d}}, {{b}, {d}}, {{a, b}, {c, d}}}
*)
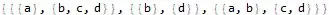
lis3 = {{{a, a}, {b, c, d}}, {{a, b}, {b, c}}};? – kglr Jan 20 '20 at 19:35