How to avoid mistakes when drawing Gaussian curvature image of explicit function?

Question

I've got a way to calculate Gaussian curvature from here (which was written by J. M.). But when I applied it to the following function, I got a lot of error messages.

GaussianCurvature[f_, {u_, v_}] := 
  Simplify[(Det[{D[f, {u, 2}], D[f, u], D[f, v]}] Det[{D[f, {v, 2}], 
         D[f, u], D[f, v]}] - 
      Det[{D[f, u, v], D[f, u], 
         D[f, v]}]^2)/(D[f, u].D[f, u] D[f, v].D[f, 
          v] - (D[f, u].D[f, v])^2)^2];

Options[gccolor]=DeleteCases[Options[ParametricPlot3D],\
ColorFunctionScaling\[Rule]_];
(gccolor[f_, {u_, ura__}, {v_, vra__}, opts : OptionsPattern[]] := 
   Module[{cf = OptionValue[ColorFunction], gc}, 
    If[cf === Automatic, cf = ColorData["ThermometerColors"]];
    gc[u_, v_] = GaussianCurvature[f, {u, v}];
    ParametricPlot3D[f, {u, ura}, {v, vra}, 
     ColorFunction -> 
      Function[{x, y, z, u, v}, cf[1/(1 + Exp[-2 gc[u, v]])]], 
     ColorFunctionScaling -> False, 
     Evaluate[FilterRules[{opts}, Options[gccolor]]], 
     Lighting -> "Neutral"]]) // Quiet

gccolor[{x, 
   y, (x^4 - 6 x^2 y^2 + y^4)/(x^2 + y^2)^2 BesselJ[4, 
     17 Sqrt[x^2 + y^2]]} /. {x -> u, y -> v}, {u, -1, 1}, {v, -1, 1}]

How can I modify these codes to avoid corresponding errors (such as replacing 1 / 0. Curvature with 10 ^ 5).

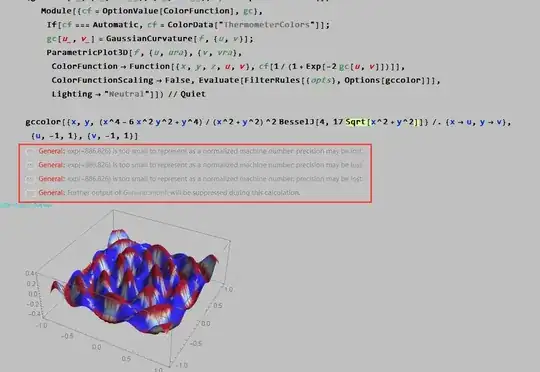
The errors you are seeing are due to a change in version 12 regarding the handling of underflow, see e.g. this. You might consider increasing the WorkingPrecision setting if this bothers you. — J. M.'s missing motivation, Jan 30 '20 at 02:43
In version 12.0, I set SetSystemOptions["CheckMachineUnderflow"->False], this setting disable detection of machine underflow.Thank you very much. — A little mouse on the pampas, Jan 30 '20 at 03:15

score 2 · Accepted Answer · answered Jan 30 '20 at 02:26

2

J. M. is in limbo♦ code seems to work when sections not commented out.

MMA v11.2

answered Jan 30 '20 at 02:26

Manuel --Moe-- G

1,057
1
8
16

I'm not sure why the OP commented out that line either. O well. In any case, it looks like I need to do better at localizing variables; I'll have to think about this. – J. M.'s missing motivation Jan 30 '20 at 02:33
Did you turn off the general warning message? – A little mouse on the pampas Jan 30 '20 at 02:54
2

Manuel is working in 11.2, which did not have the underflow trouble you are seeing in version 12. – J. M.'s missing motivation Jan 30 '20 at 02:54

How to avoid mistakes when drawing Gaussian curvature image of explicit function?

1 Answers1

Related