If I have an expression involving a variable x, like 2x+1, and I have a list of different possible x values, like {1,2,3}, is there a short way to "map" the expression over the list, returning a new list? This is one way I found:
(2x+1) /. x -> # & /@ {1,2,3}
But that has a lot of symbols in between the (2x+1) and the {1,2,3}. Is there a shorter way?
The expression might not necessarily be distributive over a list so (2x+1) /. x -> {1,2,3} won't work.
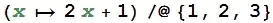
Function[x, 2 x + 1] /@ {1, 2, 3}suit your needs? How aboutTable[2 x + 1, {x, {1, 2, 3}}]? – J. M.'s missing motivation Jan 30 '20 at 04:18#,/@symbols, you could always writeReplaceAll[(2 x + 1), x -> {1, 2, 3}]– Nasser Jan 30 '20 at 04:33Tablemethod seems much more readable. Thanks. – Adrian Jan 30 '20 at 04:57