1

I was using the same code in previous version of Mathematica but unfortunately I had to update Mathematica to version 12 because I upgraded MacOS to Catalina. Now when I run my code, I get this error enter image description here

And my plots all look smeared up because of numerical errors which I wasn't seeing before. Can anyone help me how to proceed?

Whole code is here: 

ClearAll["Global`*"]
q := 1.6*10^-19; (* Electron charge in Coulomb *)

me := 9.1*10^-31; (* Free electron rest mass in kg *)

h := 6.63*10^-34;  (* Reduced Planck's constant in J.s *)

kb := 1.38*10^-23; (* Boltzmann constant in J/K *)

FD[d_, \[Eta]_] := -PolyLog[
    d + 1, -E^\[Eta]];(* Defining the Fermi-Dirac integrals *)

Nc[d_, gs_, gv_, meff_, T_] := 
  gs*gv*((2*\[Pi]*meff*me*kb*T)/h^2)^(d/
   2);  (* Effective band-edge DOS in d dimensions *)

n[d_, gs_, gv_, meff_, T_, \[Eta]F_] := 
  Nc[d, gs, gv, meff, T]*
   FD[(d - 2)/
    2, \[Eta]F]*(100)^-d; (* Effective SI carrier density in d \
dimensions in cm units*)
\[Eta]S[d_, gs_, gv_, meff_, T_, v_, nd_] := 
 Quiet[Chop[
     FindRoot[
      1/2*(n[d, gs, gv, meff, T, \[Eta]] + 
          n[d, gs, gv, meff, T, \[Eta] - (q*v)/(kb*T)]) == 
       nd, {\[Eta], 1000000}]][[1]][[
   2]]]; (* Source Fermi Level at voltage v in d dimensions*)

Lkcore[d_, gs_, gv_, meff_, T_, v_, 
  nd_] := ((FD[d/2, \[Eta]S[d, gs, gv, meff, T, v, nd]] + 
     FD[d/2, \[Eta]S[d, gs, gv, meff, T, v, nd] - (q*v)/(kb*T)] - 
     2*FD[d/2, \[Eta]S[d, gs, gv, meff, T, 0, nd]])/(FD[(d - 1)/
      2, \[Eta]S[d, gs, gv, meff, T, v, nd]] - 
     FD[(d - 1)/
      2, \[Eta]S[d, gs, gv, meff, T, v, nd] - (q*v)/(kb*T)])^2); 
(* Quantum Inductance Kernel *)

Lk0[d_, gs_, gv_, meff_, T_] := (\[Pi]*meff*me*d)/(
  q^2*Nc[d, gs, gv, meff, T]);
Lkall[d_, gs_, gv_, meff_, T_, v_, nd_] := 
  Lk0[d, gs, gv, meff, T]*Lkcore[d, gs, gv, meff, T, v, nd];
t1 = LogLogPlot[{Lkall[3, 2, 1, 1, temp, 0.1, 10^16]*10^21}, {temp, 
   0.001, 300}, Frame -> True, FrameTicks -> True, 
  GridLines -> Automatic, 
  FrameLabel -> {"Temp (K)", 
    "\!\(\*SubscriptBox[\(L\), \(k, 3  D\)]\) /l(nH/\[Mu]m)"}, 
  BaseStyle -> {FontSize -> 15}, PlotRange -> Full, 
  AxesOrigin -> {Automatic, 0}, 
  PlotLegends -> {"\!\(\*SuperscriptBox[\(10\), \
\(16\)]\)/\!\(\*SuperscriptBox[\(cm\), \(3\)]\)"}, 
  PlotStyle -> {Thick, Red}]

Result looks like this enter image description here

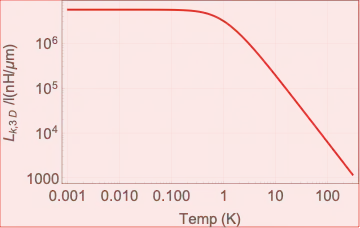
Earlier it used to look like this: enter image description here

Please help me.

Indeterminate
  • 601
  • 3
  • 9
  • Yes, version 12 now handles underflow differently; see e.g. this. – J. M.'s missing motivation Feb 03 '20 at 15:38
  • Thanks, but how do I turn off the arbitrary precision in version 12? SetSystemOptions["CatchMachineUnderflow" -> False]; doesn't work, right? – Indeterminate Feb 03 '20 at 15:43
  • @J.M.isinlimbo Rather, how should I set Underflow in version 12 to be same as my earlier version? any help is appreciated. Need this to work for a conference coming up soon :( – Indeterminate Feb 03 '20 at 15:49
  • 1
    My experience with version 12 is very limited, so someone else will have to look into it. At worst, you may have to borrow a computer with 11.x. – J. M.'s missing motivation Feb 03 '20 at 15:52
  • Can you point out which part of the code produces the underflow? I tried running the code as is, and it produces an error, but then it just churns for a long time, and I didn't have time to let it run, or to isolate the source of the problem myself. If you do your own troubleshooting and isolate the problem further, then more help might be forthcoming. – MarcoB Feb 03 '20 at 17:46
  • @MarcoB What error are you seeing? The code should not run for longer than 4-5 minutes – Indeterminate Feb 03 '20 at 18:05
  • @MarcoB I think the problem is with the FD function where I have used exponential inside the PolyLog, how can I modify it? – Indeterminate Feb 03 '20 at 18:30

0 Answers0