How do I evaluate the terms in an expression, but not the expression itself?

Question

I am trying to write a set of homework questions.

I would like the output to evaluate the constants but not the sum, so that I may present the homework question as something like this:

$$\sum_{n=1}^{340}(-4n^2-n+3)$$

Here's what I have:

c1 = RandomInteger[{-5, 5}];
c2 = RandomInteger[{-5, 5}];
c3 = RandomInteger[{-5, 5}];
c4 = RandomInteger[{1, 50}]*20
f[x_] := c1*x^2 + c2*x + c3 
f[n] 
(* 340
   3 - n - 4 n^2 *)

Defer[Sum[f[n], {n, 1, c4}]]

$\sum _{n=1}^{\text{c4}} f(n)$

It seems like I am not using Defer correctly. How can I fix this?

score 10 · Answer 1 · answered Mar 15 '13 at 19:59

10

You just need to make sure that f and c4 are evaluated. This can be done in several ways, one of which was shown by Mark. Another equally valid approach is to use With to inject the evaluated form inside the held expression:

With[{f = f[n], c4 = c4}, Defer[Sum[f, {n, 1, c4}]]]

answered Mar 15 '13 at 19:59

rm -rf

88,781
21
293
472

i would bump up your answer if I could.. but I need better reputation. thank you rm-rf thx for your help.. much appreciated – userX Mar 15 '13 at 20:01
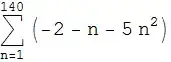
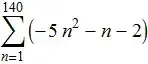
Everyone has their favorite approach, although, I note that Evaluate doesn't work here. – Mark McClure Mar 15 '13 at 20:03
@MarkMcClure Although I usually use With, I almost posted an answer that was exactly the same as yours when you submitted it... so I scrapped it and went ahead with With :) Btw, what did you mean re: Evaluate? – rm -rf Mar 15 '13 at 20:07
Oftentimes, Evaluate is used for this sort of thing, e.g. Plot[Evaluate[list],___], where list might involve a Table or some such. In this problem, you can't wrap Evaluate around the f[n]. – Mark McClure Mar 15 '13 at 20:14
@MarkMcClure Yeah, Evaluate won't work in this case because it is too deep in the expression. – rm -rf Mar 15 '13 at 20:16

score 8 · Answer 2 · answered Mar 15 '13 at 19:56

8

Defer blocks evaluation of the entire input expression, so f[n] stays as f[n]. You want to evaluate certain subparts of the expression but not the whole thing. One way to achieve this is as follows:

Defer[Sum[#1, {n, 1, #2}]]&[f[n], c4]

or, if you want traditional ordering of the polynomial,

Defer[Sum[#1, {n, 1, #2}]] &[TraditionalForm[f[n]], c4]

The first part (up to and including the ampersand &) is a pure function of two variables. The rest indicates that you're plugging f[n] and c4 into that function. Since they initially lie outside the scope of Defer, they are evaluated to what you want and then plugged in.

answered Mar 15 '13 at 19:56

Mark McClure

32,469
3
103
161

thank you Mark! that works beautifully, thank you, thank you! If I may.. one more question, is there a way to force printing of polynomial in descending order? – userX Mar 15 '13 at 19:59
@userX See edit. – Mark McClure Mar 15 '13 at 20:01
i would bump up your answer if I could.. but I need better reputation. – userX Mar 15 '13 at 20:03
perfect! thank you both, much appreciated! – userX Mar 15 '13 at 20:14

score 5 · Answer 3 · answered Mar 16 '13 at 10:43

A few additional methods for you to chew on:

Block[{Defer, Sum},
  Sum[f[n], {n, 1, c4}] // Defer
]

Block[{Sum},
  Defer @@ {Sum[f[n], {n, 1, c4}]}
]

Composition[Defer, Sum] @@ {f[n], {n, 1, c4}}

Defer @ Sum @ ## & @@ {f[n], {n, 1, c4}}

Each produces:

Mathematica graphics

Or with // TraditionalForm:

Mathematica graphics

score 3 · Answer 4 · answered Mar 15 '13 at 20:30

3

I'd go for rm-rf's approach. Since that's taken though:

expr = Defer[Sum[f[n], {n, 1, c4}]];
ReplacePart[expr, # -> expr[[Sequence @@ #]]] &@{1, 1}

(but use With, not this).

answered Mar 15 '13 at 20:30

acl

19,834
3
66
91

How do I evaluate the terms in an expression, but not the expression itself?

4 Answers4