Map and Pure Function

Question

Trying to take the first item of a member and raising it to the power of the second item of the same member and then subtracting the output from the third item of the same member, the list:

{{1, 2, 5}, {2, 3, 7}, {4, 6, 3}}

I got to as far as:

list = {{1, 2, 5}, {2, 3, 7}, {4, 6, 3}}
p = Map[#[[1]] &, list];

#[[3]] - #[[1]]^#[[2]] & /@ {{1, 2, 5}, {2, 3, 7}, {4, 6, 3}} — Rabbit, Feb 10 '20 at 00:22

score 4 · Answer 1 · answered Feb 10 '20 at 00:35

4

Another option is

list = {{1, 2, 5}, {2, 3, 7}, {4, 6, 3}}
Cases[list, {x_, y_, z_} :> x^y - z]

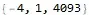
Mathematica graphics

Which I think is a little bit more readable than map

list = {{1, 2, 5}, {2, 3, 7}, {4, 6, 3}}
#[[1]]^#[[2]] - #[[3]] & /@ list

Mathematica graphics

Another option is

Function[{x, y, z}, (x^y) - z] @@@ list

Mathematica graphics

answered Feb 10 '20 at 00:35

Nasser

143,286
11
154
359

1

I think you have to multiply your results by -1. The question says that the power should be subtracted from the third element. – Shredderroy Feb 10 '20 at 01:10
One potential complication when using Cases for this purpose is that it does not necessarily preserve the order of the original list. – TimRias Feb 10 '20 at 14:42

Shredderroy · Answer 2 · 2020-02-10T01:05:19.470

2

In case you would prefer a tacit or declarative version:

{{1, 2, 5}, {2, 3, 7}, {4, 6, 3}} // (
    Map[{Last, Most /* Apply[Power]} /* Through /* Apply[Subtract]]
)
(* {4, -1, -4093} *)

edited Feb 10 '20 at 01:05

answered Feb 10 '20 at 00:59

Shredderroy

5,249
17
26

score 2 · Answer 3 · answered Feb 10 '20 at 06:59

2

mat={{1, 2, 5}, {2, 3, 7}, {4, 6, 3}};
Table[mat[[i,3]]-(mat[[i,1]]^mat[[i,2]]),{i,3}]

Or

Table[mat[[i,3]]-(mat[[i,1]]^mat[[i,2]]),{i,Length[mat]}]

answered Feb 10 '20 at 06:59

Charles Dörre

81
6

Map and Pure Function

3 Answers3