Breaking a Kinked line into $(n-1)$ segments of equal Euclidean distance?

Question

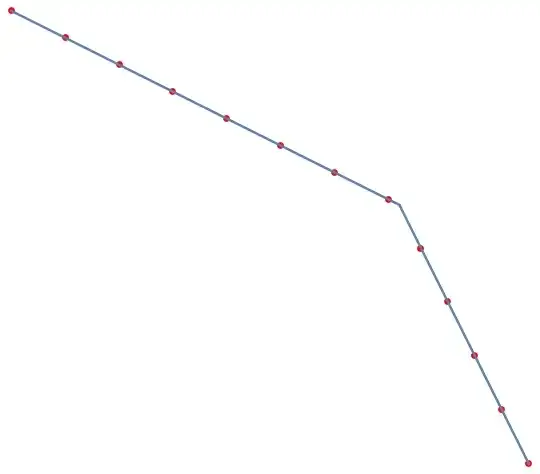
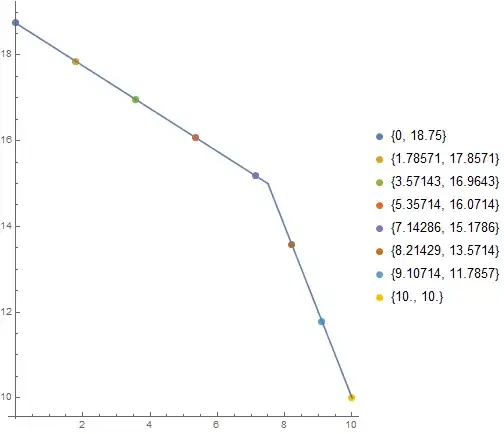
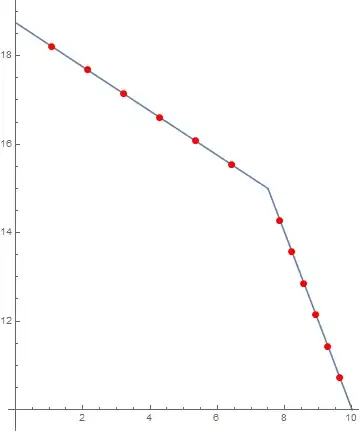
I'm wondering if anyone has a nice solution for breaking a kinked line into $(n-1)$ segments of equal euclidean distance?

Here is a MWE of my attempt. I think it does the job, and I'm sure the code can be improved, but I'm wondering if there is an much more simple/elegant way to do the job

topslope = .5;
botslope = 2;
kinkptX = 7.5;
kinkptY = 15;

kLine[x_]:=Piecewise[{{(kinkptY+kinkptX topslope)-topslope x,x<=kinkptX},{(kinkptY+kinkptX botslope)-botslope x,x>kinkptX}}]

(*Get Euclidean length of line *)
dist = Module[{xint},
   xint = Solve[kLine[x] == 0, x][[1, 1, 2]]; 
   EuclideanDistance[{xint, 0}, {kinkptX, kLine[kinkptX]}] + 
    EuclideanDistance[{kinkptX, kLine[kinkptX]}, {0, kLine[0]}]
   ];

(*note: n is number of points, which will give (n-1) segments *)
makePieces[n_] :=
 Module[{dist1, pLen, a, lowdist, ptForRdist, rKpt, rLpt, ptForLdist, 
   highdist, xint},
  dist1 = dist/(n - 1) ;
  xint = Solve[kLine[x] == 0, x][[1, 1, 
     2]];(*divide by n-1 to get n-1 equal length segments, 
  consisting of n points *)
  ptForRdist = 
   Solve[EuclideanDistance[{xint, 0}, {x, kLine[x]}] == dist1 && 
      kinkptX <= x < xint, x][[1, 1, 
     2]]; (*this point is used to find the distance between points on \
portion of the line to the right of the kink *)
  ptForLdist = 
   Solve[EuclideanDistance[{0, kLine[0]}, {x, kLine[x]}] == dist1 && 
      0 < x < kinkptX, x][[1, 1, 
     2]];(*this point is used to find the distance between points on \
portion of the line to the left of the kink *)
  highdist = ptForLdist - 0; (* 
  this gives distance between points on upper portion *)
  lowdist = 
   xint - ptForRdist; (*this gives distance between points on lower \
portion *)
  a = {};
  For[i = kinkptX; t = 0, i <= xint, i = i + lowdist, 
   AppendTo[a, xint - t]; t = t + lowdist];
  rKpt = Last[a];(*point to the right of the kink *)
  rLpt = Solve[
     EuclideanDistance[{rKpt, kLine[rKpt]}, {kinkptX, 
          kLine[kinkptX]}] + 
        EuclideanDistance[{kinkptX, kLine[kinkptX]}, {x, kLine[x]}] ==
        dist1 && 0 <= x < kinkptX, x][[1, 1, 2]];
  For[i = rLpt, i >= 0, i = i - highdist, AppendTo[a, i]];
  a
  ]

makePieces[4]

(note: the above needs to be modified to better deal with if solve encounters no solutions, since you can't take parts of {}

Answer 1

Easy. This is the function of the arc length of the graph of kLine measured from the origin.

L[y_] = Integrate[Sqrt[1 + kLine'[x]^2], {x, 0, y}, Assumptions -> y > 0];

Now one can obtain the point y such that L[y] equals a desired length with FindRoot:

desiredlength = 8;
y0 = y /. FindRoot[L[y] == desiredlength, {y, 0, 10}, Method -> "Brent"];

Test for accuracy:

Abs[L[y0] - desiredlength]

0.

Here the full subdivision:

n = 12;
S = y /. FindRoot[L[y] == #, {y, -1, 12}, Method -> "Brent"] &;
t = S /@ Subdivide[0., L[10], n];

Show[
 Graphics[{PointSize[Medium], Red, Point[{#, kLine[#]} & /@ t]}],
 Plot[kLine[x], {x, 0, 10}]
 ]

Answer 2

You can also use the function LineScaledCoordinate (from the "GraphUtilities`" package) as follows:

Needs["GraphUtilities`"]

pnts = Table[{x, kLine[x]}, {x, 0, 10, 10^-3}];
n = 7;
coords = LineScaledCoordinate[pnts, N@#] & /@ Subdivide[n]

{{0, 18.75}, {1.78571, 17.8571}, {3.57143, 16.9643}, {5.35714, 16.0714}, {7.14286, 15.1786}, {8.21429, 13.5714}, {9.10714, 11.7857}, {10., 10.}}

To verify that coords divides the line into equal-length segments, construct Lines taking successive pairs and inserting the kink in the segment it belongs and check ArcLength of each segment:

kink = 7.5;
ArcLength /@ Line /@ (Replace[Partition[coords, 2, 1], 
   {p1 : {a_, _}, p2 : {b_, _}} /; a <= kink < b :> {p1, {kink, kLine@kink}, p2}, All])

{1.99649, 1.99649, 1.99649, 1.99649, 1.99649, 1.99649, 1.99649}

Show[ListPlot[List /@ coords, BaseStyle -> PointSize[Large], 
  PlotLegends -> Placed[{coords}, Right]], Plot[kLine[x], {x, 0, 10}],
  AspectRatio -> Full]

Update: An alternative approach extracting coordinates of mesh points from graphics output produced using options MeshFunctions and Mesh:

n = 7;
plt = Plot[ArcLength[{x, kLine[x]}, {x, 0, k}], {k, 0, 10}, 
  MeshFunctions -> {#2 &}, Mesh -> n - 1, 
  MeshStyle -> Directive[Red, PointSize[Large]], AspectRatio -> Full]

Get the x-coordinates of points and add the end points 0 and 10:

xcoords = Join[{0}, Cases[Normal @ plt, Point[x_] :> x[[1]], All], {10}];
coords2 = Sort[{#, kLine@#} & /@ xcoords ];

Chop[coords2 - coords, 10^-6]

{{0, 0}, {0, 0}, {0, 0}, {0, 0}, {0, 0}, {0, 0}, {0, 0}, {0, 0}}

Note: Incidentally, a more straightforward approach using ArcLength as the mesh function in Plot of kLine does not work: Somehow, Plot divides each piece of the piecewise function into n segments:

n = 7;
Plot[kLine[k], {k, 0, 10}, MeshFunctions -> {ArcLength}, 
 Mesh -> n - 1, MeshStyle -> Directive[Red, PointSize[Large]], 
 AspectRatio -> Full]