Plot nested integration of an InterpolatingFunction efficiently

Question

Suppose we have an InterpolatingFunction from NDSolve

L = 5;

sol = First@NDSolve[{D[u[x, t], t] == D[u[x, t], {x, 2}], u[x, 0] == 0, 
      u[-5, t] == Sin[t], u[5, t] == 0}, u, {x, -L, L}, {t, 0, 10}]

Defining the functions:

int1st[x_?NumericQ, t_?NumericQ] := NIntegrate[D[Evaluate[u[s, t] /. sol], s]*Cot[(π (x - s))/(2*L)], {s, -L, x, L}, Method -> "PrincipalValue"];

intNest[x_?NumericQ, t_?NumericQ] := NIntegrate[D[Evaluate[u[xp, t] /. sol], xp]*int1st[xp, t]*Cot[(π (x - xp))/(2*L)], {xp, -L, x, L}, Method -> "PrincipalValue"];

which are, respectively, similar to the circular Hilbert transform of a periodic function and its nest (please see the section 'Hilbert transform on the circle' on that webpage). Note in intNest, int1st is called with xp as its argument, which acts as the variable of integration of intNest.

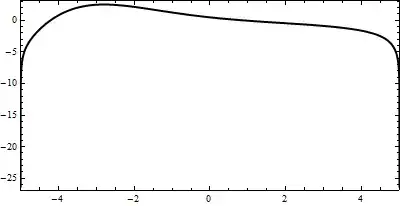
For example, plotting int1st at tn=5; I obtain the curve within 25s.

tn=5;
Plot[int1st[x,tn], {x, -L, L}, PlotRange -> {{-L, L}, All}, ImageSize -> 400, PlotPoints -> 60, AspectRatio -> 0.5, Frame -> True, Axes -> False, PlotStyle -> {Black, Thick}]

My problem is on intNest: when plotting it, there is no warning but my computer runs for hours without output. Is my definition of the intNest correct. If correct, how to make it more efficient?

Plot[intNest[x, tn], {x, -L, L}, PlotRange -> {{-L, L}, All}, ImageSize -> 400, PlotPoints -> 60, AspectRatio -> 0.5, Frame -> True, Axes -> False, PlotStyle -> {Black, Thick}]

After reading this post, I modified the function definitions:

ClearAll[int1st, intNest];

Block[{x, t}, int1st[x_?NumericQ, t_?NumericQ] = NIntegrate[D[u[s, t] /. sol, s]*Cot[(π (x - s))/(2*L)], {s, -L, x, L}, Method -> "PrincipalValue"]];

Block[{x, t}, intNest[x_?NumericQ, t_?NumericQ] = NIntegrate[D[u[xp, t] /. sol, xp]*int1st[xp, t]*Cot[(π (x - xp))/(2*L)], {xp, -L, x, L}, Method -> "PrincipalValue"]];

Findings: int1st can be plotted well in about 20s (same result as above), but it is still very slow to plot intNest.

Answer 1

Update: Used the built-in "InterpolationPointSubdivision" method.

Update 2: Memoization helps because the subdivision is at the same points (given by xcoords in the code below) every time. So in intNest2[], the call int1st2[xp, t] will initially be made at the same xp for each subinterval, unless the subinterval contains the singular point x. I say, "initially," because the recursive subdivision of each subinterval in the intNest2[] call may be different depending on the value of x and its effect on the complete integrand.

Some explanation in the comments. If I have more time, I might be able to add more:

L = 5;

(* OP's *)
ClearAll[int1st, intNest];
int1st[x_?NumericQ, t_?NumericQ] := 
  NIntegrate[
   Derivative[1, 0][u /. sol][s, t]*
    Cot[(π (x - s))/(2*L)], {s, -L, x, L}, 
   Method -> "PrincipalValue"];

intNest[x_?NumericQ, t_?NumericQ] := 
  NIntegrate[
   D[Evaluate[u[xp, t] /. sol], xp]*int1st[xp, t]*
    Cot[(π (x - xp))/(2*L)], {xp, -L, x, L}, 
   Method -> "PrincipalValue"];

(* with singularity removed from NIntegrate and 
 * manual interpolating nodes subdivision *)
ClearAll[int1st2, intNest2];

(* interpolating nodes *)
{xcoords, tcoords} = u["Coordinates"] /. sol;

mem : int1st2[x_?NumericQ, t_?NumericQ] :=
  mem = Block[{s}, (* memoization seems to help with Plot[] *)
    With[{
      du = Derivative[1, 0][u /. sol],
      dux = Derivative[1, 0][u /. sol][x, t]},
     NIntegrate[
       Piecewise[{{du[s, t]*Cot[(π (x - s))/(2*L)] - 
           dux (2*L)/(π (x - s)), x != s}}], (* subtract singular part *)
       {s, -L, x, L},
       Method -> {"InterpolationPointsSubdivision", (* divide interval at nodes *)
         "SymbolicProcessing" -> 0},
       PrecisionGoal -> 4 (* PDE solution is low-precision *)
       ] + dux ( (2*L) Log[(L + x)/(L - x)])/π (* add PV integral of singular part *)
     ]];

intNest2[x_?NumericQ, t_?NumericQ] := 
  Block[{xp}, 
   With[{
     du = Derivative[1, 0][u /. sol], 
     dux = Derivative[1, 0][u /. sol][x, t]*int1st2[x, t]}, 
    NIntegrate[
      Piecewise[{{du[xp, t]*int1st2[xp, t]*
           Cot[(π (x - xp))/(2*L)] - dux (2*L)/(π (x - xp)), 
         x != xp}}], {xp, -L, x, L}, 
      Method -> {"InterpolationPointsSubdivision", 
        "SymbolicProcessing" -> 0}, PrecisionGoal -> 4] + 
     dux*((2*L) Log[(L + x)/(L - x)])/π]];

Single-call timings:

int1st2[4, 5] // Quiet // AbsoluteTiming
int1st[4, 5] // AbsoluteTiming
(*
  {0.017778, -1.6291}
  {0.056669, -1.6291}
*)

intNest2[4, 5] // AbsoluteTiming
intNest[4, 5] // AbsoluteTiming
(*
  {5.96797, 1.78776}
  {52.9943, 1.78775}
*)
Plot[int1st2[x, 5], {x, -L, L}, PlotRange -> {{-L, L}, All}, 
  ImageSize -> 400, PlotPoints -> 60, AspectRatio -> 0.5, 
  Frame -> True, Axes -> False, 
  PlotStyle -> {Black, Thick}] // AbsoluteTiming

There are 441 points here, so multiply by the single call timings to get an estimate of the time to plot:

Cases[%, Line[p_] :> Length@p, Infinity]
(*  {441}  *)

The nested integral is still going to be slow. You can use options like PlotPoints and MaxRecursion to reduce the number of points plotted (that is, reduce the number of function calls).