0

I am trying to solve following differential equation $$\frac{d^2y}{dx^2}+(a+\frac{2}{\pi}b\hspace{3pt}\tan^{-1}x)\hspace{2pt}y=0$$ To solve it in mathematica I wrote the following code 

s = ParametricNDSolveValue[{y''[x] + (a + b*((2/Pi)*ArcTan[x]))*
  y[x] == 0, y[-10] == Exp[I*10*Sqrt[a + b]], y'[-10] == (-I)*Sqrt[a + b]*Exp[I*10*Sqrt[a + b]]}, y, {x, -10, 10}, {a, b}]

but I am getting following error where am I making the mistake?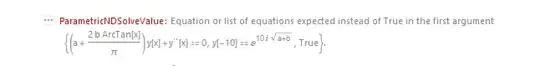enter image description here

aitfel
  • 177
  • 5
  • Works just fine. Try to Quit your Kernel and restart. Look at the last boundary condition, this evaluated to True – user21 Feb 26 '20 at 09:42
  • @user21 thanks. So is it a normal practice to restart the kernel when faced with such problem? – aitfel Feb 26 '20 at 09:45
  • @no. This just a quick test. Somewhere you defined something (a variable perhaps) that made the last bc evaluate to True. When you need to reuse a variable as a symbol use Clear or ClearAll – user21 Feb 26 '20 at 09:52

0 Answers0