Efficiently finding spheres furthers apart along and perpendicular to a given direction

Question

Setting

I am dealing with a box of spheres, all having the same radius and inserted into a finite box size without any overlaps. Along a given direction $\mathbf v$, I am trying to find:

• (a) The two spheres $i,j$ whose difference vectors $\mathbf r= \mathbf r_i-\mathbf r_j$ is parallel to $\mathbf v$ and are furthest apart. That is, among the pairs of spheres that satisfy $\mathbf r \parallel \mathbf v,$ which pair has the largest $|r|.$

• (b) Similarly, the two spheres furthest apart whose difference vector is now perpendicular to $\mathbf v.$ That is, among the pairs of spheres that satisfy $\mathbf r \perp \mathbf v,$ which pair has the largest $|r|.$

Regarding the thresholds with which we deem two normalized vectors $\mathbf u, \mathbf v$ to be parallel or perpendicular:

• $\mathbf u \parallel \mathbf v$ iff $\mathbf u\cdot \mathbf v \ge 0.9,$ let's call these cases type=1,
• $\mathbf u \perp \mathbf v$ iff $\mathbf u\cdot \mathbf v \le 0.1.$, let's call these cases type=-1,
• and anything else we'll call type=0.

---

Attempt

What I have managed to do so far is:

• First create a list spherespairs of all possible pairs using Subset, and a n-by-n matrix matdists of all zeros to be filled with pairwise distances, where n is the number of spheres.
• Defined a function furthest that takes two spheres, the target vector $\mathbf v$ (targetvec in the code), and computes their Euclidean distance (and updates matdists), their normalized difference vector and its inner product with $\mathbf v$ and the obtained type.
• Then I apply furthest to all the possible pairs.
• With the former, to find (a), I'd then first filter pairs whose type=1, then find the one with largest dist. Similarly for (b).

Working example and code:

Initialization:

spheres = {};
n = 200; (*number of spheres*)
r = 0.5; (*radius*)
boxlen = 20; (*cubic box length*)
targetvec = {0., 0., 1.}; (*this is our direction vector v*) 

Inserting the spheres randomly and without overlap:

SeedRandom[120];
While[Length[spheres] < n, s = RandomReal[{r, boxlen - r}, 3];
  If[And @@ (Norm[# - s] > 2*r & /@ spheres), AppendTo[spheres, s]]];

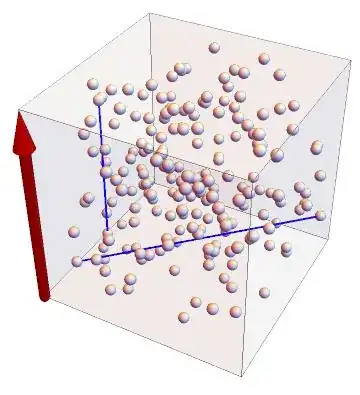
Visualisation of spheres and in red arrow the given vector $\mathbf v:$

cube = {Opacity[0.1], Cuboid[{0, 0, 0}, {boxlen, boxlen, boxlen}]};
Graphics3D[{cube, 
  Sphere[#, r] & /@ spheres, {Red, Arrowheads[0.1], 
   Arrow[Tube[{{0, 0, 0}, targetvec*boxlen}, r]]}}, Boxed -> False]

List of all sphere pairs and initialization of matrix of distances:

spherepairs = Subsets[spheres, {2}];
matdists = ConstantArray[0, {n, n}];

The described function furthest:

furthest[sphere1_, sphere2_, targetvec_, boxsize_] := 
  Module[{r1 = sphere1, r2 = sphere2, v = targetvec, l = boxsize},
   r = Normalize[r1 - r2];
   innerprod = r.v;
   dist = Norm[r1 - r2];
   indexsphere1 = Flatten@Position[spheres, r1];
   indexsphere2 = Flatten@Position[spheres, r2];
   matdists[[indexsphere1[[1]], indexsphere2[[1]]]] = dist;
   matdists[[indexsphere2[[1]], indexsphere1[[1]]]] = dist;
   type = 0;
   Which[Abs[innerprod] >= 0.9,
    type = 1;,
    Abs[innerprod] <= 0.1,
    type = -1;,
    True,
    type = 0;
    ];
   {type, innerprod, dist}
   ];

Applying the function to all the pairs:

result = furthest[#1, #2, targetvec, boxlen] & @@@ 
  spherepairs // AbsoluteTiming

which takes about $6$ seconds for $n=200$ spheres!

---

Problem and question:

• My approach seems to scale very inefficiently, to obtain the type, innerprod and dist of all possible pairs (all stored in result) takes about $6$ seconds for only $200$ particles, and I haven't even proceeded to filtering result to solve (a) and (b). Later I will have to do these calculations for systems of $n\approx 2000,$ so efficiency in finding (a) and (b) is of essence. I know my approach is really naive because I calculate everything for all pairs, as opposed to targetting my search to cases likely to be furthest apart. But I don't know how I could achieve such a targeted search! Any hints would be really helpful.

• In my approach, is there any part where I am doing something completely inefficiently considering Mathematica's capabilities? In other words, is there a simple change from which my approach would benefit a major speed-up? I have a feeling my approach is really over-killing it...

Answer 1

Follows a script which determines with assigned accuracy the furthers parallel and perpendicular set of points.

distmin = 0;
distminp = 0;
e1 = 0.01;
e2 = 0.01;
e3 = 0.01;
For[i = 1, i <= n, i++, 
 For[j = i + 1, j <= n, 
  j++, {dx, dy, dz} = spheres[[i]] - spheres[[j]]; 
  If[Abs[dx/dz] < e1 && Abs[dy/dz] < e2, dist = dx^2 + dy^2 + dz^2; 
   If[dist > distmin, distmin = dist; imax = i; jmax = j]];
  l0 = dx^2 + dy^2;
  lpro = Sqrt[l0];
  If[Abs[dz/lpro] < e3, len = l0 + dz^2; 
   If[len > distminp, distminp = len; iperp = i; jperp = j]]
  ]
 ]

If[distmin == 0 || distminp == 0, Print["Tolerances must be loosened"],
  v1 = spheres[[imax]] - spheres[[jmax]];
  v2 = spheres[[iperp]] - spheres[[jperp]];
  Print[v1.v2/Norm[v1]/Norm[v2]];
  gr1 = ParametricPlot3D[spheres[[imax]] mu + spheres[[jmax]] (1 - mu),{mu, 0, 1}, PlotStyle -> {Thick, Blue}];
  gr2 = ParametricPlot3D[spheres[[iperp]] mu + spheres[[jperp]] (1 - mu),{mu, 0, 1}, PlotStyle -> {Thick, Blue}];
  Show[gr0, gr1, gr2]
]

NOTE

Given a direction vector $\vec v$ the points should be previously rotated such that the $z$ axis direction coincides with $\vec v$ direction.