How to create a custom EdgeShapeFunction whose arrowheads snap to vertices

Question

When using the Graph option PerformanceGoal -> "Quality", the endpoints of edges (arrows) will snap to vertices, no matter the vertex shape or size.

Example:

Graph[
 {"apple" -> "banana", "banana" -> "watermelon",
  "watermelon" -> "apple", "apple" -> "watermelon"}, 
 VertexShapeFunction -> Function[{point, vertex, size}, Text[Framed@vertex, point]],
 PerformanceGoal -> "Quality"
 ]

---

I am looking to change the EdgeShapeFunction so directed reciprocal edges will always be straight.

This is the effect I am looking to achieve:

Graph[{1 -> 2, 2 -> 3, 3 -> 1, 1 -> 3},
 EdgeShapeFunction -> 
  Function[{coord, edge}, Arrow[{First[coord], Last[coord]}]],
 PerformanceGoal -> "Quality"
 ]

However, using a custom edge shape function disables the snapping effect. This is bad because depending on the vertex size, even circular vertices can obscure arrowheads. Example:

Graph[{1 -> 2, 2 -> 3, 3 -> 1, 1 -> 3},
 EdgeShapeFunction -> 
  Function[{coord, edge}, Arrow[{First[coord], Last[coord]}]],
 PerformanceGoal -> "Quality",
 VertexSize -> 1/4
 ]

Question: Is there a way to define a custom EdgeShapeFunction without disabling this spanning effect? Is there a built-in edge shape function which always draws straight lines? Built-ins do not disable the snapping effect.

I know that for this specific use case, the arrowhead could be offset manually to avoid overlapping with circular vertices. But I am looking for a solution that works with arbitrary vertex shapes, such as the one in my first example. At this time, I am only looking for straight edge shape functions, not fancy ones, so any solution specific to straight ones is still acceptable.

---

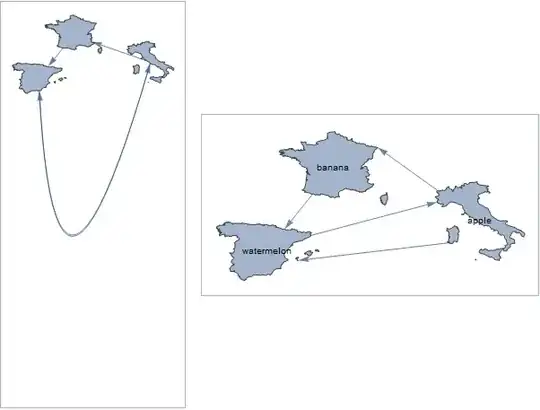
This is a hack that sort of works for visualization, but it is ugly, inflexible, and does not allow one to keep working with Graph:

Show@Graph[{"apple" -> "banana", "banana" -> "watermelon", 
    "watermelon" -> "apple", "apple" -> "watermelon"}, 
   VertexShapeFunction -> 
    Function[{point, vertex, size}, Text[Framed@vertex, point]], 
   PerformanceGoal -> "Quality"] /. 
 Arrow[BezierCurve[{first_, ___, last_}]] :> Arrow[{first, last}]

Answer 1

ClearAll[eSF]
eSF[g_] := Function[{coord, edge}, 
   With[{dl1 = "VertexID$" <> ToString[VertexIndex[g, edge[[1]]]], 
     dl2 = "VertexID$" <> ToString[VertexIndex[g, edge[[2]]]]}, 
    Arrow[{DynamicLocation[dl1, Automatic, Center], 
      DynamicLocation[dl2, Automatic, Center]}]]];

Examples:

SeedRandom[1]
g1 = Graph[{1 -> 2, 2 -> 3, 3 -> 1, 1 -> 3}, 
   PerformanceGoal -> "Quality",  
   VertexSize :> RandomReal[{.1, .4}], 
   VertexStyle -> Opacity[.1]];

g2 = Graph[{"apple" -> "banana", "banana" -> "watermelon", 
    "watermelon" -> "apple", "apple" -> "watermelon"}, 
   VertexShapeFunction -> Function[{point, vertex, size}, Text[Framed@vertex, point]], 
   PerformanceGoal -> "Quality"];

Row[Graph[#, EdgeShapeFunction -> eSF[#], ImageSize -> Medium] & /@ {g1, g2}]

SeedRandom[1]
vsizes = Thread[{"apple", "banana", "watermelon"} -> RandomReal[{.1, .5}, 3]];
cpn = AssociationThread[{"apple", "banana", "watermelon"}, RandomInteger[{3, 7}, 3]];

g3 = Graph[{"apple" -> "banana", "banana" -> "watermelon", 
    "watermelon" -> "apple", "apple" -> "watermelon"}, 
   VertexShapeFunction -> Function[{point, vertex, size}, 
     Polygon@CirclePoints[point, First@size, cpn@vertex]], 
   PerformanceGoal -> "Quality", VertexSize -> vsizes];

Row[{Graph[g3, ImageSize -> Medium], 
  Graph[g3, EdgeShapeFunction -> eSF[g3], ImageSize -> Medium]}]

Update: With a slight modification, we can play with the third argument of DynamicLocation to avoid edge overlaps:

ClearAll[eSF2]
eSF2[g_, pos_: {Center, Center}] := Function[{coord, edge}, 
   With[{dl1 = "VertexID$" <> ToString[VertexIndex[g, edge[[1]]]], 
     dl2 = "VertexID$" <> ToString[VertexIndex[g, edge[[2]]]]}, 
    Arrow[{DynamicLocation[dl1, Automatic, pos[[1]]], 
      DynamicLocation[dl2, Automatic, pos[[2]]]}]]];

Example:

SeedRandom[77]
vsizes = Thread[Range[3] -> RandomReal[{.1, .5}, 3]];
g4 = Graph[{1 -> 2, 2 -> 3, 3 -> 1, 1 -> 3}, 
  PerformanceGoal -> "Quality", VertexSize -> vsizes, 
  VertexStyle -> Opacity[.1]]; 

Graph[g4, EdgeShapeFunction ->
   {DirectedEdge[1, 3] -> eSF2[g4, {{1, .7}, {-1, .7}}], 
   DirectedEdge[3, 1] -> eSF2[g4, {{-1, -.2}, {1, .2}}]}, 
 ImageSize -> Medium]

Update 2: Arbitrary polygons as vertex shapes (per M.R.'s suggestion in comments):

polygons = Entity["Country", #]["Polygon"] & /@ {"Italy", "France", "Spain"};
maps = AssociationThread[{"apple", "banana", "watermelon"}, polygons];

g5 = Graph[{"apple" -> "banana", "banana" -> "watermelon", 
    "watermelon" -> "apple", "apple" -> "watermelon"}, 
   VertexShapeFunction -> Function[{point, vertex, size}, 
     Scale[Translate[maps[vertex], point], size]], 
   PerformanceGoal -> "Quality", VertexSize -> 1, ImageSize -> Medium];

Row[Panel /@ {g5, Graph[g5, VertexLabels -> Placed["Name", Center], 
    EdgeShapeFunction -> 
      {DirectedEdge["watermelon", "apple"] -> eSF2[g5, {{1, .7}, {Left, .7}}], 
      DirectedEdge["apple", "watermelon"] -> eSF2[g5, {{Left, Bottom}, {1, -.5}}], 
      DirectedEdge["apple", "banana"] -> eSF2[g5, {Center, {1, 1}}]}, 
    ImageSize -> Medium]}, Spacer[10], Alignment -> Center]