Why the difference in performance? Array vs List and `Delete` vs `Nothing`

Question

In a previous question I was warned against the use of Nothing to delete elements from a list, and rather use Delete. Being of an inquisitive nature, I investigated the performance hit when using Nothing instead of Delete

n = 300;
data2 = Table[0.0, n, 500, 18]  (* Create some data. This is more-or-less the shape and quantity of my real-life data. *)

timing = {{"Nothing[]", "Delete[]"}}; (* Create a list to contain the timing data *)
For[j = 0, j < 50, j++,  (* Run 50 trials of timing measurements *)
 data3 = data2; (* Create a copy of the data *)
 i = RandomInteger[{1, n}, {10, 1}]; (* Select the elements that should be deleted *)
 ii = Flatten[i];
 t1 = AbsoluteTiming[data3[[ii]] = Nothing; data3 = data3;]; (* Delete the data using Nothing, and time it. *)
 data3 = data2; (* Use the original data again *)
 t2 = AbsoluteTiming[data3 = Delete[data3, i];]; (* Delete the data using Delete[], and time it. *)
 AppendTo[timing, {First[t1], First[t2]}] (* Record the times *)
 ]
ListPlot[{timing[[2 ;;, 1]], timing[[2 ;;, 2]]}, ImageSize -> Large, 
 PlotLegends -> timing[[1]], 
 AxesLabel -> {"Trial no.", "AbsoluteTiming"}, 
 PlotLabel -> "Single delete"]

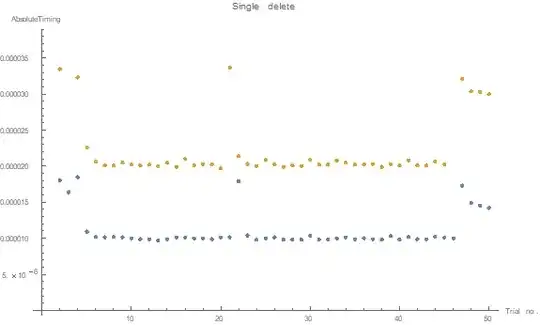
(In the plots below the blue markers represent the Nothing method and the yellow markers Delete.)

As can be expected, the Nothing method is much slower than Delete, and the story should end here. But this did not agree with my experience using other data. After spending too much of my employer's time on finding out what the differences are exactly, I found that replacing a single element of the data with something arbitrary (data2 [[3]] = x) turns data2 from an array into a list of lists, and this makes Nothing perform better than Delete.

But the real surprise is that both seem to be orders of magnitude faster when operating on the 'list of lists' than on the matrix. I imagine that Mathematica's array functions are highly efficient, so I feel that I am missing something. Does my test do what I think it does? Is there a better way to use Delete, or are there better functions for deletion that I don't know of? Is there a better way to run the tests?

---

Following a suggestion in the comments, I did some more timings:

data2 = Table[0.0, n, 500, 18];
data3 = data2 
data3[[3]] = "Data" // AbsoluteTiming
(* {1.*10^-7, "Data"} *)

data3 = data2 
data3[[3, 3, 3]] = 1. // AbsoluteTiming 
(* {1.*10^-7, 1.} *)

But

data3 = data2 
data3[[3]] = {data2[[2]]} ; // AbsoluteTiming 
(* {0.0432838, Null} *)
data3 = data2 
data3[[3]] = data2[[2]] ; // AbsoluteTiming 
(* {0.0134969, Null} *) 

This is how I would expect it: copying parts of arrays is much more efficient than copying lists.

More relevant perhaps are the memory requirements:

|          | ByteCount | LeafCount |
|----------|-----------|-----------|
|data2     |21 600 160 | 2 850 301 | 
|data3     |72 989 696 | 2 840 801 | 

So for the deletion problem above, the trade-off is speed for memory.

Answer 1

data2[[3]] = x; // AbsoluteTiming might give a hint.

I explain it to myself as follows: At that point when you execute data2[[3]] = x, all rows other than row 3 are internally copied to packed arrays and data2 is replaced by a list of pointers to those. Now all following operations are performed with an array of pointers. Of course, this is significantly faster as the packed arrays with the actual data do not have to be touched at all ...

However, this comes at a price: The output is no more a packed array, so subsequent operations on it may be slowed down.