I want to check my homework answers. So I am wondering if there is a way you can find Fourier series using mathematica of this function g(x)=x(1-x) on interval [0,1)? If so, can someone please show me how you can using Mathematica?
Asked
Active
Viewed 137 times
1
1 Answers
3
It is important to say what the period is. Taking the period as 1 in your case, then your function looks like
g[x_] := Piecewise[{{x (1 - x),
0 <= x < 1}, {-x (1 + x), -1 <= x < 0}, {0, True}}];
Plot[g[x], {x, -1, 1}]
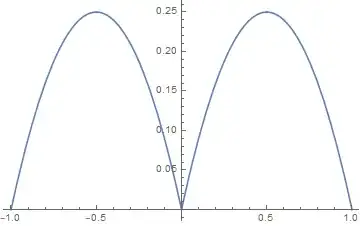
The above assumes even periodic extension. To find the Fourier series now use
fs = FourierSeries[g[x], x, 3, FourierParameters -> {1, -2 Pi}];
fs // ExpToTrig
Plot[{g[x], fs}, {x, 0, 1}]
$$ -\frac{\cos (2 \pi x)}{\pi ^2}-\frac{\cos (4 \pi x)}{4 \pi ^2}-\frac{\cos (6 \pi x)}{9 \pi ^2}+\frac{1}{6} $$
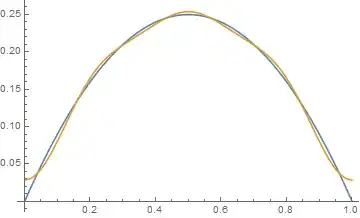
More terms produces better approximation
fs = FourierSeries[g[x], x, 7, FourierParameters -> {1, -2 Pi}];
fs // ExpToTrig
Plot[{g[x], fs}, {x, 0, 1}]
$$ -\frac{\cos (2 \pi x)}{\pi ^2}-\frac{\cos (4 \pi x)}{4 \pi ^2}-\frac{\cos (6 \pi x)}{9 \pi ^2}-\frac{\cos (8 \pi x)}{16 \pi ^2}-\frac{\cos (10 \pi x)}{25 \pi ^2}-\frac{\cos (12 \pi x)}{36 \pi ^2}-\frac{\cos (14 \pi x)}{49 \pi ^2}+\frac{1}{6} $$

Nasser
- 143,286
- 11
- 154
- 359
rst=easyFourierSinSeries[x(1-x),{x,0,1}]; Plot[{x(1-x),rst/.C->2//ReleaseHold}//Evaluate,{x,0,1}]. – xzczd Mar 16 '20 at 06:15