I am attempting to solve the equation
with the Wolfram one-liner
NDSolve[{D[ρ[y, t]] == D[D[ρ[y, t], y], y], ρ[-1, t] == 10, ρ[1, t] == 10,ρ[y, 0] == 0},
ρ, {y, -1, 1}, {t, 0, 10}]
However, this threw a NDSolve::ibcinc warning that the initial and boundary conditions conflicted, as I didn't properly implement the inequalities on the initial and boundary conditions. How could I specify the inequalities on "t" properly to return a physical solution? I have searched through the Mathematica Stack Exchange to no avail for this issue.
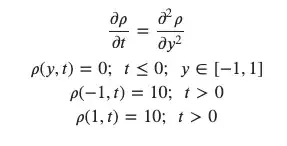
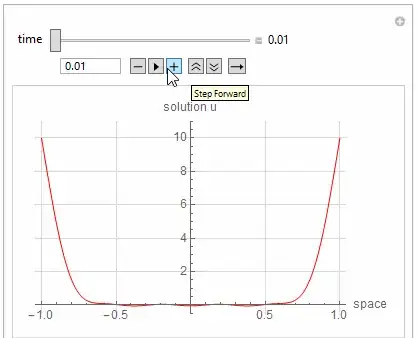
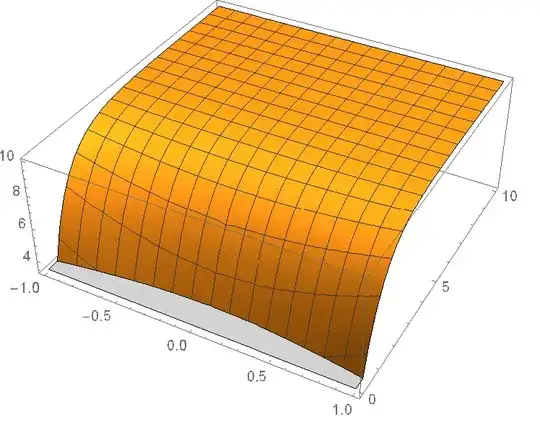
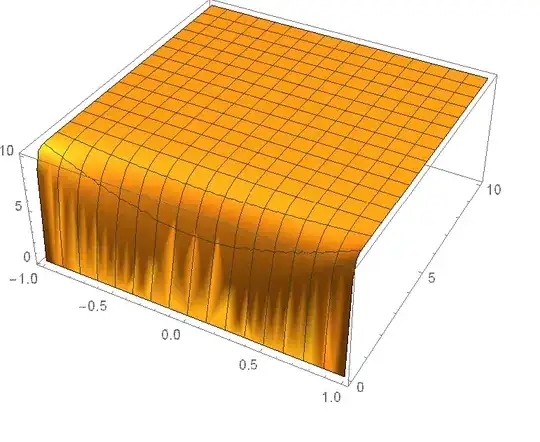

[Rho][-1, t] == 10 (1-Exp[-10 t]), [Rho][1, t] == 10 (1-Exp[-10 t])– Alex Trounev Mar 20 '20 at 14:13D[\[Rho][y, t]]should beD[\[Rho][y, t],t]. Then, "I have searched through the Mathematica Stack Exchange to no avail for this issue." you should have searched harder. Strongly related, if not duplicate: https://mathematica.stackexchange.com/a/127411/1871 To be more specific, add e.g.Method -> {"MethodOfLines", "DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100}}toNDSolve. – xzczd Mar 21 '20 at 02:38