Solving CROSS TIES automatically

Question

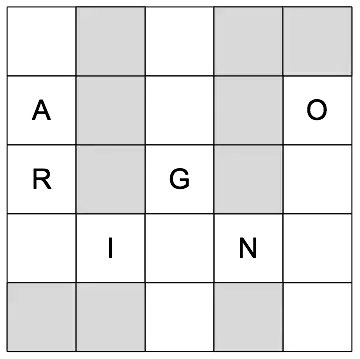
A clever puzzle in the Sunday New York Times Magazine is CROSS TIES (by Will Shortz). You are given a $5 \times 5$ grid with some squares filled with letters, others grayed out, and yet others white. The puzzle is to fill in the remaining white squares with letters so as to spell valid English words or names that all are examples from the same category or class.

One puzzle is shown on the left, and its solution (with red letters) is at the right:

It is a fairly straightforward Mathematica search to find all dictionary words that fit the constraints of a given word, for example:

DictionaryLookup["w"~~_~~"is"~~_]

and

DictionaryLookup[_~~"o"~~_]

for two of them here.

I'm seeking an elegant method to impose all the constraints (by defining variable-letter names) so that the routine returns only the final solution words. (You can hand-code the problem-specific data for each such puzzle.)

The ideal case would be to also demand all solution words be semantically related... to enforce the semantic constraint of the problem. (Frankly, I suspect that most puzzles are so constrained that only the intended solution words will fit, but in some cases others might fit as well.)

Test your solution out on this:

Another:

Another:

---

Here's a first pass at a solution, admittedly a bit ugly and efficient, and not in a Mathematica style.

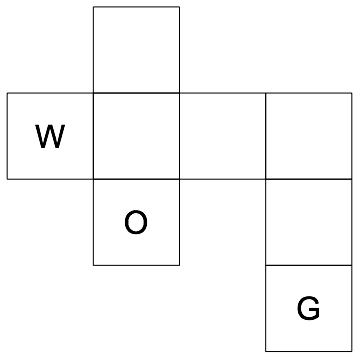
Consider a simple but relevant example:

Then something like:

solutions = {};
words = {DictionaryLookup["w" ~~ _ ~~ _ ~~ _],
   DictionaryLookup[_ ~~ _ ~~ "o"],
   DictionaryLookup[_ ~~ _ ~~ "g"]};

Table[
  If[(StringTake[words[[1, i]], {2}] == 
     StringTake[words[[2, j]], {2}]) && 
    (StringTake[words[[1, i]], {4}] == 
     StringTake[words[[3, k]], {1}]), 
   AppendTo[solutions, {words[[1, i]], words[[2, j]], words[[3, k]]}]],
  {i, Length[words[[1]]]},
  {j, Length[words[[2]]]},
  {k, Length[words[[3]]]}
  ];

solutions

Surely there is a more elegant way to perform this...